奥本海姆信号与系统第二版课后题答案
奥本海姆《信号与系统》(第2版)笔记和课后习题答案详解
1.整理名校笔记,浓缩内容精华。 总结了教材重难点内容,参考国内名校名师讲授该教材的课堂笔记,整理量该教材的知识精华。
2.解析课后习题,提供详尽答案。 参考大量信号与系统相关资料,对奥本海姆《信号与系统》第2版的课后习题进行了详细的分析和解答。
3.精选考研真题,巩固重难点知识。 为了强化对重要知识点的理解,精选了部分名校近年的信号与系统考研真题,基本涵盖了每章的考点和难点,特别注重理论联系实际,凸显当前热点。
立即阅读 >>
奥本海姆《信号与系统》(第2版)教材章节课后习题答案解析
1-1 用笛卡儿坐标形式(x+yj)表示下列复数。
ejπ/2,e-jπ/2,ejπ/2,e-jπ/2,ej5π/2,![]() ,
,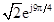 ,
,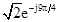 ,
,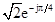
解:利用欧拉公式:

和复平面性质
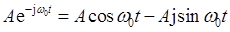
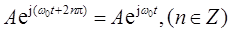
有:
ejπ/2=(cosπ)/2+(jsinπ)/2=-1/2,e-jπ/2=(cosπ)/2-(jsinπ)/2=-1/2
ejπ/2=cos(π/2)+jsin(π/2)=j,e-jπ/2=cos(π/2)-jsin(π/2)=-j
ej5π/2=ejπ/2=cos(π/2)+jsin(π/2)=j
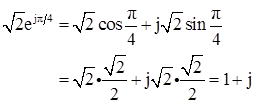
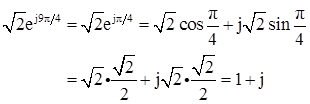
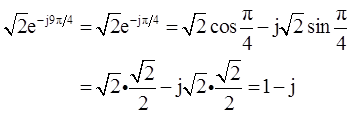

【总结】笛卡儿坐标形式(x+yj)表示复数的时候,核心是找到对应的实部x和虚部y。大多数情况需要利用到欧拉公式ejθ=cosθ+jsinθ展开,另外虚指数信号具有周期性,也就是ejθ=ej(θ±2mπ)=cosθ+jsinθ。
1-2 用极坐标形式(rejθ,-π<θ≤π)表示下列复数。
5,-2,-3j,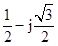 ,1+j,(1-j)2,j(1-j),(1+j)/(1-j),
,1+j,(1-j)2,j(1-j),(1+j)/(1-j),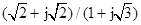
解:根据5,-2,-3j,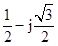 ,1+j,(1-j)2,j(1-j),(1+j)/(1-j),
,1+j,(1-j)2,j(1-j),(1+j)/(1-j),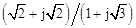
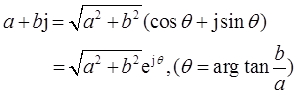
有:
5=5cos0+5jsin0=5ej0
-2=2cosπ+2jsinπ=ejπ
-3j=3cos(-π/2)+j3sin(-π/2)=3e-jπ/2
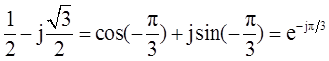
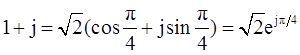
(1-j)2=-2j=2cos(-π/2)+j2sin(-π/2)=2e-jπ/2
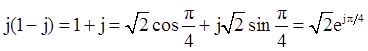
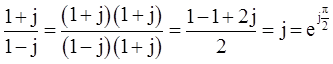
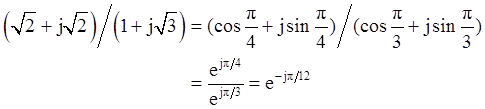
1-3 对下列每一个信号求P∞和E∞。
(a)x1(t)=e-2tu(t)。
(b)x2(t)=ej(2t+π/4)。
(c)x3(t)=cos(t)。
(d)x1[n]=(1/2)nu[n]。
(e)x2[n]=ej[π/(2n)+π/8]。
(f)x3[n]=cos(πn/4)。
解:(a)

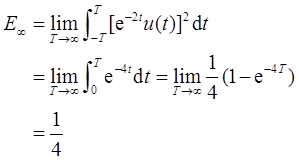
(b)
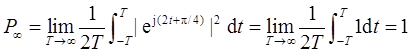
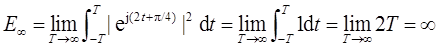
(c)
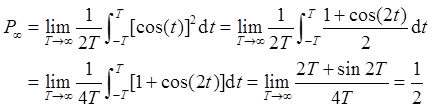
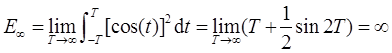
(d)

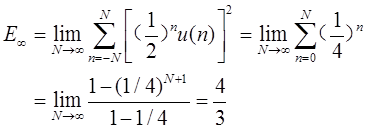
(e)
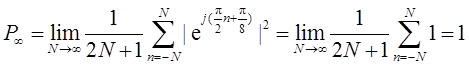
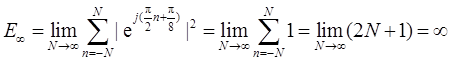
(f)

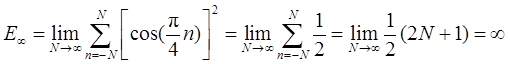
【总结】连续时间信号和离散时间信号的能量和功率的计算公式不一样。
对于连续时间信号:能量
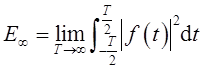
功率

对于离散时间信号:能量

功率
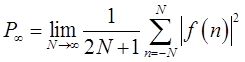
1-4 设n<-2和n>4时x[n]=0,对以下每个信号确定其值保证为零的n值。
(a)x[n-3]。
(b)x[n+4]。
(c)x[-n]。
(d)x[-n+2]。
(e)x[-n-2]。
解:(a)x[n-3]=0,(n-3)<-2或(n-3)>4,即x[n-3]=0,n<1或n>7。
(b)x[n+4]=0,(n+4)<-2或n+4>4,即x[n+4]=0,n<-6或n>0。
(c)x[-n]=0,(-n)<-2或(-n)>4,即x[-n]=0,n<-4或n>2。
(d)x[-n+2]=0,(-n+2)<-2或(-n+2)>4,即x[-n+2]=0,n<-2或n>4。
(e)x[-n-2]=0,(-n-2)<-2或(-n-2)>4,即x[-n-2]=0,n<-6或n>0。
1-5 设t<3时x(t)=0,确定以下每个信号的值保证为零的t值。
(a)x(1-t)。
(b)x(1-t)+x(2-t)。
(c)x(1-t)x(2-t)。
(d)x(3t)。
(e)x(t/3)。
解:(a)x(1-t)=0,(1-t)<3,即x(1-t)=0,t>-2。
(b)x(1-t)+x(2-t)=0,(1-t)<3且(2-t)<3,即x(1-t)+x(2-t)=0,t>-1。
(c)x(1-t)x(2-t)=0,(1-t)<3或(2-t)<3,即x(1-t)x(2-t)=0,t>-2。
(d)x(3t)=0,(3t)<3,即x(3t)=0,t<1。
(e)x(t/3)=0,(t/3)<3,即x(t/3)=0,t<9。
1-6 判断下列信号的周期性。
(a)x1(t)=2ej(t+π/4)u(t)。
(b)x2[n]=u[n]+u[-n]。
(c)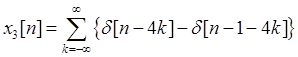
解:(a)由于存在u(t),也就是只有t>0的时候x1(t)才有图像,因此一定是非周期的。
(b)由于
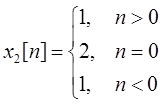
所以x2[n]也不具备周期性。
(c)

因此根据周期函数用卷积表示的方法判断出,x3[n]的周期为4。
1-7 对以下每个信号求信号的偶部保证为零的所有自变量值。
(a)x1[n]=u[n]-u[n-4]。
(b)x2(t)=sin(t/2)。
(c)x3[n]=(1/2)nu[n-3]。
(d)x4(t)=e-5tu(t+2)。
解:(a)
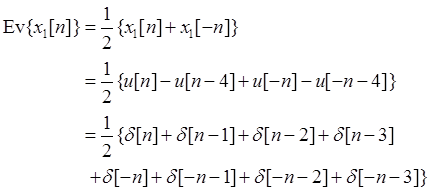
只有当|n|>3时,Ev{x1[n]}=0。
(b)Ev{x2(t)}=(1/2)·{sin(t/2)+sin(-t/2)}=(1/2)·{sin(t/2)-sin(t/2)}=0;即对一切t,Ev{x2(t)}=0。
(c)
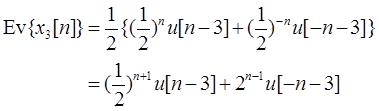
由于
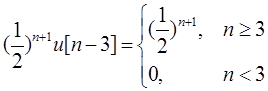
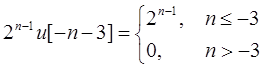

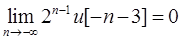
所以当|n|<3及|n|切有时,Ev{x3[n]}=0
(d)Ev{x4(t)}=(1/2)·{e-5tu(t+2)+e5tu(-t+2)},由于
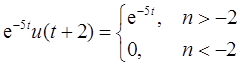
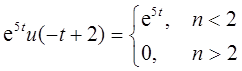
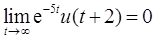
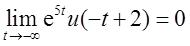
所以只有当|t|有当时,Ev{x4(t)}=0。
| 内容来源 | 奥本海姆信号与系统第2版课后习题答案 |
扫码阅读 |
1-8 将下列信号的实部表示成Ae-atcos(ωt+f)的形式,其中A,a,ω和f都是实数,A>0且-π<f≤π。
(a)x1(t)=-2。
(b)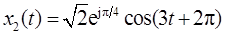
(c)x3(t)=e-tsin(3t+π)。
(d)x4(t)=je(-2+j100)t。
解:(a)Re{x1(t)}=x1(t)=2e-0·tcos(0·t+π),即A=2,a=0,ω=0,Φ=π。
(b)
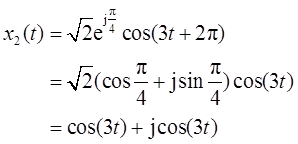
即Re{x2(t)}=cos(3t)=e-0·tcos(3t+0),即A=1,a=0,ω=3,f=0。
(c)x3(t)=e-tsin(3t+π)=e-tsin(3t+π/2+π/2)=e-tcos(3t+π/2)
Re{x3(t)}=x3(t)=e-tcos(3t+π/2),即A=1,a=1,ω=3,Φ=π/2。
(d)x4(t)=je(-2+j100)t=e-2tej(100t+π/2)=e-2tcos(100t+π/2)+e-2tjsin(100t+π/2)
Re{x4(t)}=1·e-2tcos(100t+π/2),即A=1,a=2,ω=100,Φ=π/2。
1-9 判断下列信号的周期性。若是周期的,给出它的基波周期。
(a)x1(t)=jej10t。
(b)x2(t)=e(-1+j)t。
(c)x3[n]=ej7πn。
(d)x4[n]=3ej3π(n+1/2)/5。
(e)x5[n]=3ej(3/5)(n+1/2)。
解:(a)x1(t)=jej10t=ej(10t+π/2)=cos(10t+π/2)+jsin(10t+π/2),故x1(t)为周期信号,基波周期T=2π/10=π/5。
(b)x2(t)=e(-1+j)t=e-t·ejt=e-tcos(t)+je-tsin(t),故x2(t)不是周期信号。
(c)x3[n]=ej7πn=cos(7πn)+jsin(7πn)⇒ω0/(2π)=7π/(2π),即m/N=7/2,故x3[n]是周期序列,基波周期N=2。
(d)
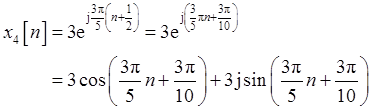
则ω0/(2π)=(3π/5)/(2π)=3/10,即m/N=3/10,故x4[n]是周期序列,基波周期N=10。
(e)x5[n]=3ej(3/5)(n+1/2)=3ej(3n/5+3/10)=3cos(3n/5+3/10)+3jsin(3n/5+3/10),又ω0/(2π)=(3/5)/(2π)=3/(10π),为无理数,故x5[n]不是周期序列。
1-10 求信号x(t)=2cos(10t+1)-sin(4t-1)的基波周期。
解:由于cos(10t+1)和sin(4t-1)都为周期信号,且ω1=10,ω2=4,ω1:ω2=5:2=m1:m2,故x(t)的基波周期为:T=mi·(2π/ωi)=5×2π/10(或2×2π/4)=π。
1-11 求信号x[n]=1+ej4πn/7-ej2πn/5的基波周期。
解:对于ej4πn/7,其ω1=4π/7,ω1/(2π)=2/7为有理数,所以ej4πn/7是周期信号。同样,ej2πn/5中ω2=2π/5,ω2/(2π)=1/5为有理数,故ej2πn/5也是周期信号。又ej4πn/7的基波周期N1=7,ej2πn/5的基波周期N2=5,N1与N2的最小公倍数为35,所以x[n]的基波周期为N=35。
【总结】假设f1(t)的周期为T1,f2(t)的周期为T2,f(t)=f1(t)+f2(t)为周期信号的充要条件是,T1与T2的比值为有理数,如果T1/T2=m/n,那么周期信号的周期为T=mT2=nT1。
1-12 考虑离散时间信号
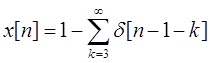
试确定整数M和n0的值,以使x[n]可表示为
x[n]=u[Mn-n0]
解:

即M=-1,n0=-3。
1-13 考虑连续时间信号
x(t)=δ(t+2)-δ(t-2)
试对信号
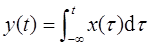
计算E∞值。
解:由于单位冲激响应和单位阶跃响应之间的微积分关系,因此
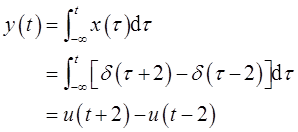
根据能量的公式
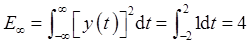
……
完整版链接:
上册:http://dacai.100xuexi.com/Ebook/993228.html
下册:http://dacai.100xuexi.com/Ebook/992970.html
【推荐】达聪学习网 “奥本海姆《信号与系统》第2版复习笔记+课后题答案”
- 页数:598
- 推荐指数:★★★★★
- 适用:网页/电脑/平板/手机



共有 0 条评论