胡运权运筹学教程第5版课后习题答案

胡运权《运筹学教程》第5版课后习题答案解析

第一章 线性规划及单纯形法

1分别用图解法和单纯形法求解下列线性规划问题：

（1）指出问题具有唯一最优解、无穷多最优解、无界解还是无可行解；

（2）当具有有限最优解时，指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。

（1）

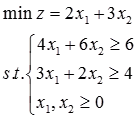
（2）

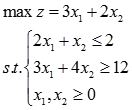
（3）

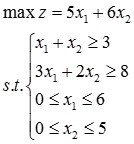
（4）

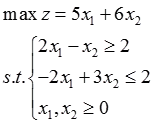
解：（1）图解法：

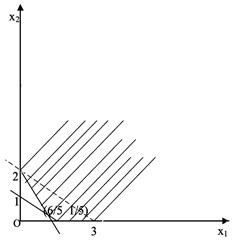
图2-1-1

当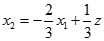经过点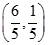时，z最小，且有无穷多个最优解。

单纯形法：

在上述问题的约束条件中令z^′＝－z，分别加入剩余变量x₃，x₄，引入人工变量x₅，x₆化为标准型：

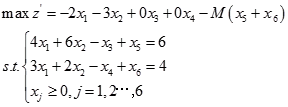
由线性规划问题的标准型可列出单纯初始形表并逐步迭代，计算结果如表2-1-1所示：

表2-1-1

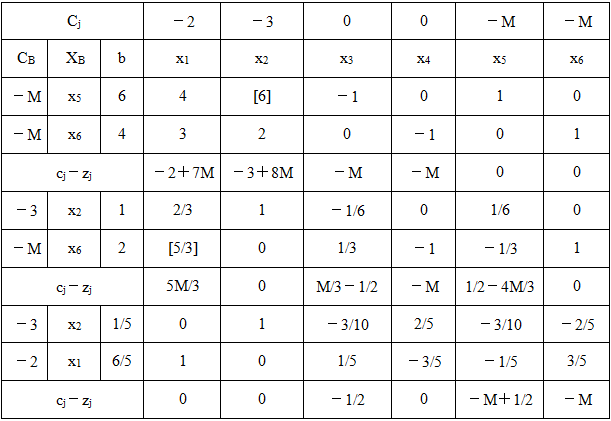
单纯形表的计算结果表明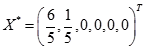，同时发现存在非基变量检验数为0，说明该线性规划问题有无穷多最优解。

（2）图解法：

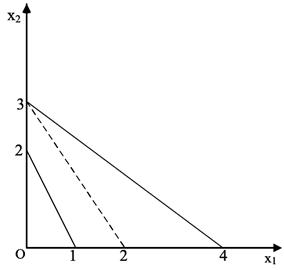
图2-1-2

在x₁，x₂≥0情况下约束条件无可行域，因此无可行解。

在图解法中已看出本例无可行解，现用单纯形法求解。在添加松弛变量和人工变量后，模型可写成

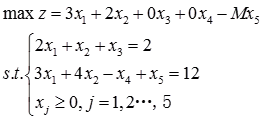
由线性规划问题的标准型可列出单纯初始形表并逐步迭代，计算结果如表2-1-2所示：

表2-1-2

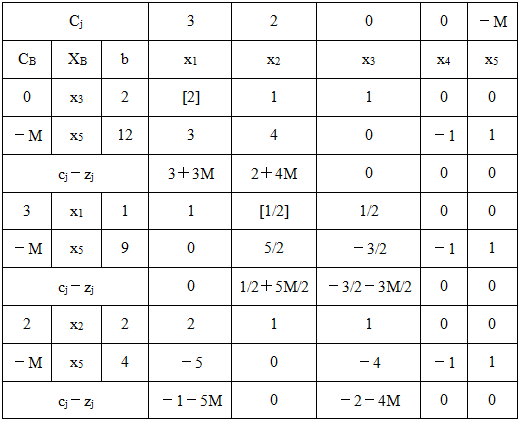
此时所有检验数均≤0，但基变量中仍含有非零的人工变量，表明问题无可行解。

（3）图解法：

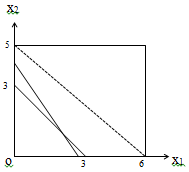
图2-1-3

当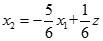经过点（6，5）时，z最大，且有唯一最优解。

单纯形法：

加入剩余变量x₃，x₄，引入人工变量x₅，x₆，加入松弛变量x₇，x₈，化为标准型如下：

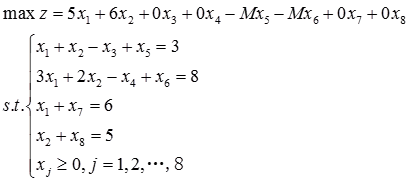
由线性规划问题的标准型可列出单纯初始形表并逐步迭代，计算结果如表2-1-3所示。

表2-1-3

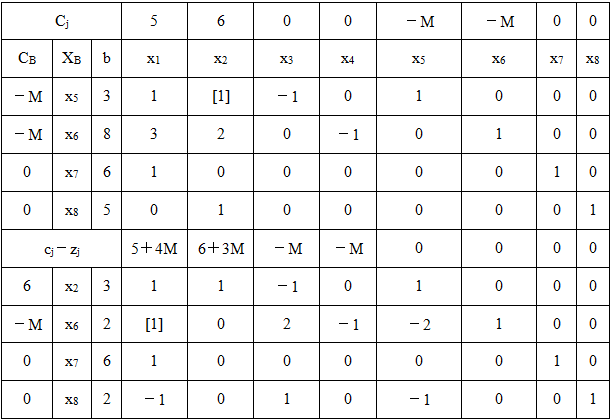
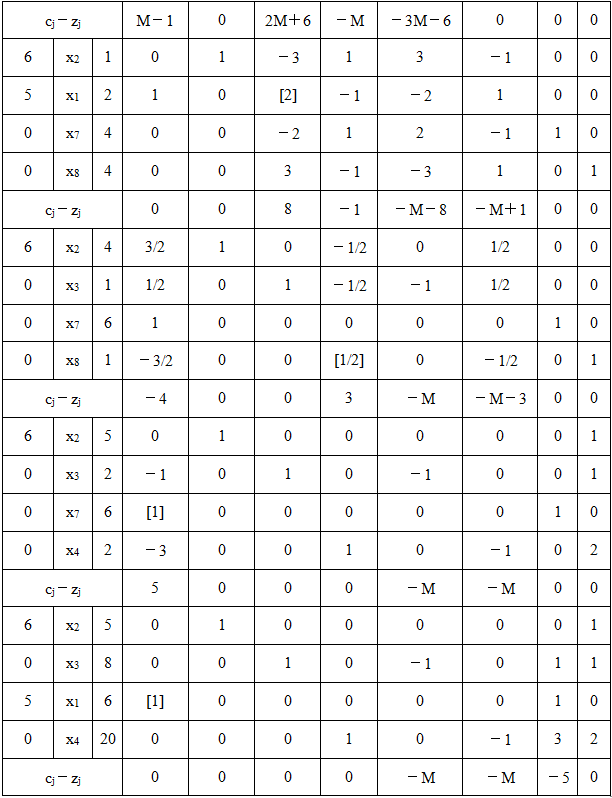
单纯形表计算结果表明X^*＝（6，5，8，20，0，0，0，0）^T，Z^*＝60。

（4）图解法求解：该问题的可行域为无界域，如图2-1-4所示。目标函数有无界解。

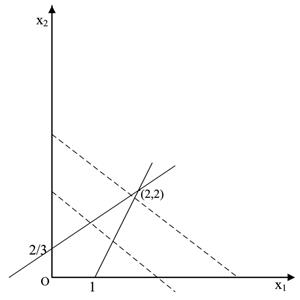
图2-1-4

单纯形法：

加入剩余变量x₃，松弛变量x₄，引入人工变量x₅，化为标准型为：

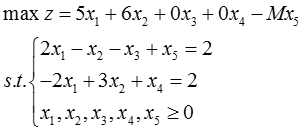
由线性规划问题的标准型可列出单纯初始形表并逐步迭代，计算结果如表2-1-4所示：

表2-1-4

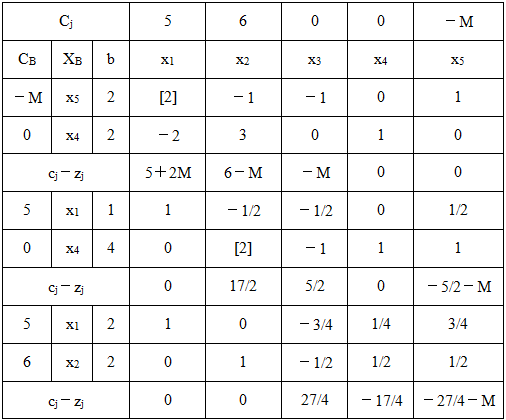
发现存在x₃检验数＞0，且这对应列向量均为负数，根据解的判别规则，说明线性规划有无界解。

内容来源

胡运权《运筹学教程》第5版真题题库

扫码阅读

2将下述线性规划问题化成标准形式。

（1）

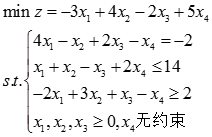
（2）

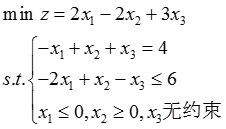
解：（1）化成标准形式：

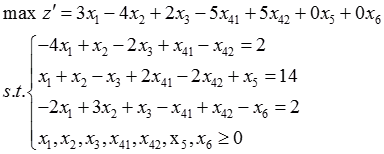
（2）化成标准形式：

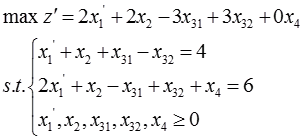
3对下述线性规划问题找出所有基解，指出哪些是基可行解，并确定最优解。

（1）

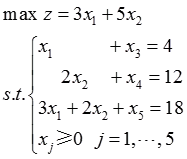
（2）

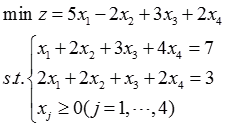
解：（1）由于约束方程组为3×5阶系数矩阵，其秩为3，其基变量可任取约束方程组中的三列，取非基变量的值为0，此时求出的基变量的值为方程的一个基解，有一个基就可以求出一个基解。设X_i（i＝1，2，3，…，8）是对应约束方程组的基变量，可知

X₁＝（x₃，x₄，x₅），令x₁＝0，x₂＝0，可求出x₃＝4，x₄＝12，x₅＝18

X₂＝（x₁，x₄，x₅），令x₃＝0，x₂＝0，可求出x₁＝4，x₄＝12，x₅＝6

X₃＝（x₁，x₃，x₄），令x₂＝0，x₅＝0，可求出x₁＝6，x₃＝－2，x₄＝12

X₄＝（x₁，x₂，x₄），令x₃＝0，x₅＝0，可求出x₁＝4，x₂＝3，x₄＝6

X₅＝（x₂，x₃，x₅），令x₁＝0，x₄＝0，可求出x₂＝6，x₃＝4，x₅＝6

X₆＝（x₁，x₂，x₃），令x₄＝0，x₅＝0，可求出x₁＝2，x₂＝6，x₃＝2

X₇＝（x₁，x₂，x₅），令x₃＝0，x₄＝0，可求出x₁＝4，x₂＝6，x₅＝－6

X₈＝（x₂，x₃，x₄），令x₁＝0，x₅＝0，可求出x₂＝9，x₃＝4，x₄＝－6

将每一个基解代入目标函数中，求出每一个对应的z值，满足约束条件x_i≥0的解为基可行解，所有基可行解中满足z值最大的解为最优解。最终计算如表2-1-5所示，其中□标示的为基可行解，*标示的为最优解。

表2-1-5

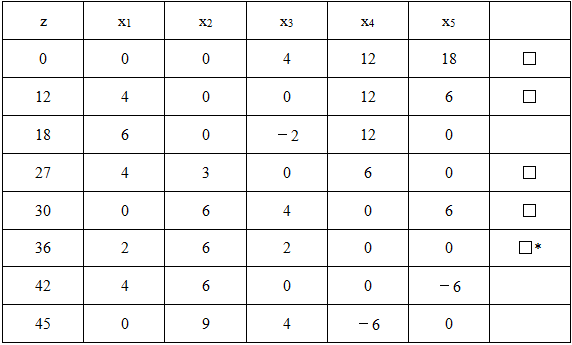
故可得方程的最优解为x₁＝2，x₂＝6，x₃＝2，x₄＝0，x₅＝0，z^*＝36

（2）该线性规划问题的标准形式为：

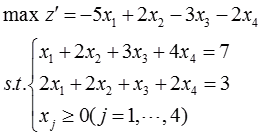
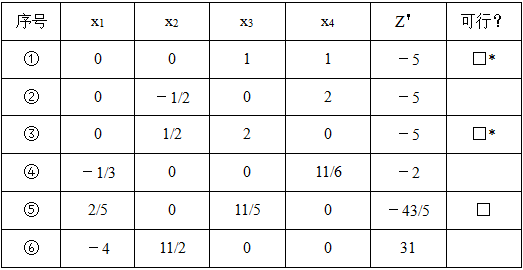
其全部基解见表2-1-6中的①～⑥，□标示的为基可行解，*标示的为最优解，z^*＝5。

表2-1-6

4题1（3）中，若目标函数变为max z＝cx₁＋dx₂，讨论c，d的值如何变化，使该问题可行域的每个顶点依次使目标函数达到最优。

解：有目标函数max z＝cx₁＋dx₂可得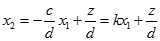：，其中。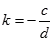

（1）当k≤0时

若c≥0，d＞0，可行域的顶点（6，5）使目标函数达到最优；

若c≤0，d＜0，－3/2≤k≤－1，可行域的顶点（2，1）使目标函数达到最优；

若c≤0，d＜0，k≤－3/2，可行域的顶点（0，4）使目标函数达到最优。

（2）当k≥0时

若c≥0，d＜0，可行域的顶点（6，0）使目标函数达到最优；

若c≤0，d＞0，可行域的顶点（0，5）使目标函数达到最优。

（3）当k不存在时

即d＝0时，若c≥0，可行域的边界x₁＝6使目标函数达到最优；

若c≤0，可行域的边界x₁＝0使目标函数达到最优。

……

 完整版链接： /Ebook/991984.html

【推荐】达聪学习网“胡运权《运筹学教程》第5版考研真题＋课后习题＋章节题库”