同济大学高等数学第七版课后习题答案

习题1-1 映射与函数【课后答案】

1求下列函数的自然定义域：

（1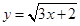）；（2）y＝1/（1－x²）；

（3）；（4）；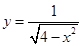

（5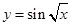）；（6）y＝tan（x＋1）；

（7）y＝arcsin（x－3）；（8）；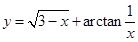

（9）y＝ln（x＋1）；（10）y＝e^1/x。

解：（1）3x＋2≥0⇒x≥－2/3，故其定义域为[－2/3，＋∞）。

（2）1－x²≠0⇒x≠±1，故其定义域为（－∞，－1）∪（－1，1）∪（1，＋∞）。

（3）x≠0且1－x²≥0⇒x≠0且|x|≤1，故其定义域为[－1，0）∪（0，1]。

（4）4－x²＞0⇒|x|＜2，故其定义域为（－2，2）。

（5）x≥0，故其定义域为[0，＋∞）。

（6）x＋1≠kπ＋π/2（k∈Z），故其定义域为{x|x∈R且x≠（k＋1/2）π－1，k∈Z}。

（7）|x－3|≤1⇒2≤x≤4，故其定义域为[2，4]。

（8）3－x≥0且x≠0，故其定义域为（－∞，0）∪（0，3]。

（9）x＋1＞0⇒x＞－1，故其定义域为（－1，＋∞）。

（10）x≠0，故其定义域为（－∞，0）∪（0，＋∞）。

2下列各题中，函数f（x）和g（x）是否相同？为什么？

（1）f（x）＝lgx²，g（x）＝2lgx；

（2）f（x）＝x，；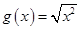

（3）；

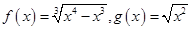（4）f（x）＝1，g（x）＝sec²x－tan²x。

解：（1）函数f（x）和g（x）不同，因其定义域不同。

（2）函数f（x）和g（x）不同，因其对应法则不同，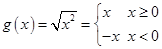

（3）函数f（x）和g（x）相同，因其定义域、对应法则均相同。

（4）函数f（x）和g（x）不同，因其定义域不同。

3设

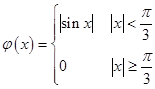
求φ（π/6），φ（π/4），φ（－π/4），φ（－2），并作出函数y＝φ（x）的图形。

解：

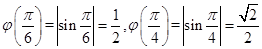
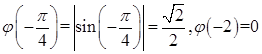
y＝φ（x）的图形如图1-2-1所示。

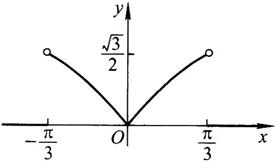
图1-2-1

4试证下列函数在指定区间内的单调性：

（1）y＝x/（1－x），（－∞，1）；

（2）y＝x＋lnx，（0，＋∞）。

证：（1）y＝x/（1－x）＝－1＋1/（1－x），（－∞，1）。

设x₁＜x₂＜1，因为

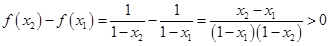
所以f（x₂）＞f（x₁），即f（x）在（－∞，1）内单调增加。

（2）设0＜x₁＜x₂，因为f（x₂）－f（x₁）＝x₂＋lnx₂－x₁－lnx₁＝x₂－x₁＋ln（x₂/x₁）＞0，可得f（x₂）＞f（x₁），所以f（x）在（0，＋∞）内单调增加。

5设f（x）为定义在（－l，l）内的奇函数，若f（x）在（0，l）内单调增加，证明f（x）在（－l，0）内也单调增加。

证：设－l＜x₁＜x₂＜0，则0＜－x₂＜－x₁＜l，因为f（x）是奇函数，所以f（x₂）－f（x₁）＝－f（－x₂）＋f（－x₁），又因为f（x）在（0，1）内单调增加，所以f（－x₁）－f（－x₂）＞0，从而f（x₂）＞f（x₁），即f（x）在（－l，0）内也单调增加。

6设下面所考虑的函数都是定义在区间（－l，l）上的。证明：

（1）两个偶函数的和是偶函数，两个奇函数的和是奇函数；

（2）两个偶函数的乘积是偶函数，两个奇函数的乘积是偶函数，偶函数与奇函数的乘积是奇函数。

证：（1）设f₁（x），f₂（x）均为偶函数，则f₁（－x）＝f₁（x），f₂（－x）＝f₂（x）。

令F（x）＝f₁（x）＋f₂（x），于是F（－x）＝f₁（－x）＋f₂（－x）＝f₁（x）＋f₂（x）＝F（x），故F（x）为偶函数。

设g₁（x），g₂（x）均为奇函数，则g₁（－x）＝－g₁（x），g₂（－x）＝－g₂（x），令G（x）＝g₁（x）＋g₂（x），于是G（－x）＝g₁（－x）＋g₂（－x）＝－g₁（x）－g₂（x）＝－G（x），故G（x）为奇函数。

（2）设f₁（x），f₂（x）均为偶函数，则f₁（－x）＝f₁（x），f₂（－x）＝f₂（x），令F（x）＝f₁（x）·f₂（x），于是F（－x）＝f₁（－x）·f₂（－x）＝f₁（x）f₂（x）＝F（x），故F（x）为偶函数。

设g₁（x），g₂（x）均为奇函数，则g₁（－x）＝－g₁（x），g₂（－x）＝－g₂（x），令G（x）＝g₁（x）·g₂（x），于是G（－x）＝g₁（－x）·g₂（－x）＝[－g₁（x）][－g₂（x）]＝g₁（x）g₂（x）＝G（x），

故G（x）为偶函数。

设f（x）为偶函数，g（x）为奇函数，则f（－x）＝f（x），g（－x）＝－g（x），令H（x）＝f（x）·g（x），于是H（－x）＝f（－x）·g（－x）＝f（x）[－g（x）]＝－f（x）·g（x）＝－H（x），故H（x）为奇函数。

7下列函数中哪些是偶函数，哪些是奇函数，哪些既非偶函数又非奇函数？

（1）y＝x²（1－x²）；（2）y＝3x²－x³；

（3）y＝（1－x²）/（1＋x²）；（4）y＝x（x－1）（x＋1）；

（5）y＝sinx－cosx＋1；（6）y＝（a^x＋a^－x）/2。

解：（1）因为f（－x）＝（－x）²[1－（－x）²]＝x²（1－x²）＝f（x），所以f（x）为偶函数。

（2）因为f（－x）＝3（－x）²－（－x）³＝3x²＋x³，f（－x）≠f（x）且f（－x）≠－f（x），所以f（x）既非偶函数又非奇函数。

（3）因为f（－x）＝（1－x（－x）²）/（1＋（－x）²）＝（1－x²）/（1＋x²）＝f（x），所以f（x）为偶函数。

（4）因为f（－x）＝（－x）[（－x）－1][（－x）＋1]＝－x（x－1）（x＋1）＝－f（x），所以f（x）为奇函数。

（5）因为f（－x）＝sin（－x）－cos（－x）＋1＝－sinx－cosx＋1，f（－x）≠f（x）且f（－x）≠－f（x），所以f（x）既非偶函数又非奇函数。

（6）因为f（－x）＝（a^－x＋a^x）/2＝f（x），所以f（x）为偶函数。

内容来源

同济大学数学系《高等数学》笔记和课后答案

扫码阅读

8下列各函数中哪些是周期函数？对于周期函数，指出其周期：

（1）y＝cos（x－2）；

（2）y＝cos4x；

（3）y＝1＋sinπx；

（4）y＝xcosx；

（5）y＝sin²x。

解：（1）是周期函数，周期l＝2π。

（2）是周期函数，周期l＝π/2。

（3）是周期函数，周期l＝2。

（4）不是周期函数。

（5）是周期函数，周期l＝π。

9求下列函数的反函数：

（1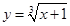）；（2）y＝（1－x）/（1＋x）；

（3）y＝（ax＋b）/（cx＋d）（ad－bc≠0）；（4）y＝2sin3x（－π/6≤x≤π/6）；

（5）y＝1＋ln（x＋2）；（6）y＝2^x（2^x＋1）。

解：（1）由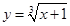解得x＝y³－1，即反函数为y＝x³－1。

（2）由y＝（1－x）/（1＋x）解得x＝（1－y）/（1＋y），即反函数为y＝（1－x）/（1＋x）。

（3）由y＝（ax＋b）/（cx＋d）解得x＝（－dy＋b）/（cy－a），即反函数为y＝（－dx＋b）/（cx－a）。

（4）由y＝2sin3x（－π/6≤x≤π/6）解得x＝arcsin（y/2）/3，即反函数为y＝arcsin（x/2）/3。

（5）由y＝1＋ln（x＋2）解得x＝e^y－1－2，即反函数为y＝e^x－1－2。

（6）由y＝2^x（2^x＋1）解得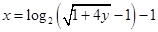，即反函数为。

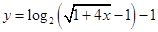10设函数f（x）在数集X上有定义，试证：函数f（x）在X上有界的充分必要条件是它在X上既有上界又有下界。

解：设f（x）在X上有界，则存在M＞0，使得|f（x）|≤M，x∈X，所以－M≤f（x）≤M，x∈X，即f（x）在X上有上界M，下界－M。

反之，设f（x）在X上有上界K₁，下界K₂，即K₂≤f（x）≤K₁，x∈X；取M＝max{|K₁|，|K₂|}，则有|f（x）|≤M，x∈X，即f（x）在X上有界。

11在下列各题中，求由所给函数构成的复合函数，并求这函数分别对应于给定自变量值x₁和x₂的函数值：

（1）y＝u²，u＝sinx，x₁＝π/6，x₂＝π/3；

（2）y＝sinu，u＝2x，x₁＝π/8，x₂＝π/4；

（3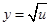），u＝1＋x²，x₁＝1，x₂＝2；

（4）y＝e^u，u＝x²，x₁＝0，x₂＝1；

（5）y＝u²，u＝e^x，x₁＝1，x₂＝－1。

解：（1）y＝sin²x，y₁＝1/4，y₂＝3/4。

（2）y＝sin2x，，y₂＝1。

（3）。

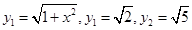（4）。

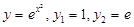（5）y＝e^2x，y₁＝e²，y₂＝e^－2。

12设f（x）的定义域D＝[0，1]，求下列各函数的定义域：

（1）f（x²）；

（2）f（sinx）；

（3）f（x＋a）（a＞0）；

（4）f（x＋a）＋f（x－a）（a＞0）。

……

 完整版链接： /Ebook/987092.html

【推荐】达聪学习网“同济大学《高等数学》（第7版）笔记和课后习题答案”