吴大正信号与线性系统分析第4版考点知识笔记教材讲义

第1章 信号与系统复习笔记

本章是信号分析与系统分析的基础，详细介绍了信号与系统的概念与分类方法以及常用的连续信号与离散信号，讨论了冲激函数和冲激偶函数的重要性质，介绍了线性时不变（LTI）系统的特性，简要介绍了LTI系统的描述方法和分析方法。

【学习重点】

（1）重点掌握信号不同分类方法的标准。

（2）掌握不同信号的时域表达式和波形。

（3）熟练运用信号的基本运算来画波形变换。

（4）重点掌握冲激函数与冲激偶函数的性质与运算。

（5）重点掌握LTI系统的特性（线性、时不变性、因果性、稳定性）。

（6）掌握根据框图来求微分方程和差分方程的方法。

一、信号的基本概念与分类

信号是带有信息（如语言、音乐、图像、数据等）的随时间和空间变化的物理量或物理现象，其图像为信号的波形。在数学上信号表示为一个时间的函数x（t），故信号与函数一般相互通用。

根据信号的不同特性，可对信号进行不同的分类：确定信号与随机信号；周期信号与非周期信号；连续时间信号与离散时间信号；实信号与复信号；能量信号与功率信号等，各自的特点见表1-1-1。

表1-1-1 信号的分类及特点

【注意】

①模拟信号抽样后变成在时间上离散的信号，但仍是模拟信号，该抽样信号必须经过量化才成为数字信号。

②

③信号f（t）在单位电阻上的能量为

它所消耗的功率为

④序列f（k）的能量定义为

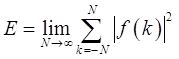
能量定义为

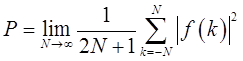
⑤周期信号判断的方法：

若信号f₁（t）和f₂（t）均为周期信号，周期分别为T₁和T₂，则信号f（t）＝f₁（t）＋f₂（t）为周期信号的前提条件是T₁/T₂＝k/m的值为有理数（k，m为互素正整数），其周期满足T＝kT₂＝mT₁，离散系统也成立。

对于正余弦信号，连续时间信号f（t）＝cos（ω₀t）的周期为2的周ω₀；离散时间信号f（k）＝cos（ω₀k）为周期信号有前提条件2为周ω₀必须为有理数。

二、信号的基本运算

信号的基本运算主要有加减法、乘法、反转、平移、尺度变换，其时域表达式与各运算的特点见表1-1-2。

表1-1-2 信号的基本运算及其特点

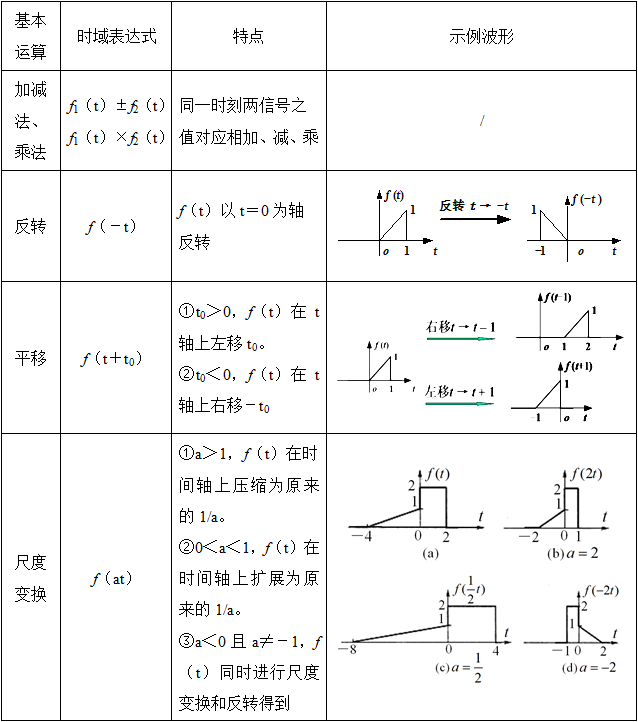
【注意】①f（t）→f（at－b）的图像变换可以有两个方法：

方法一：f（t）→f（t－b）→f（at－b），也就是先平移再尺度变换。

方法二：f（t）→f（at－b）→f（t－b），也就是先尺度变换再平移。

一般我们利用方法一画图像比较简单，另外注意f（at－b）→f（t）一般是按照方法一的逆过程也就是f（at－b）→f（t－b）→f（t）画图像。

②离散信号通常不做展缩运算。

内容来源

吴大正《信号与线性系统分析》第4版考点笔记课后答案

扫码阅读

三、典型信号及其性质

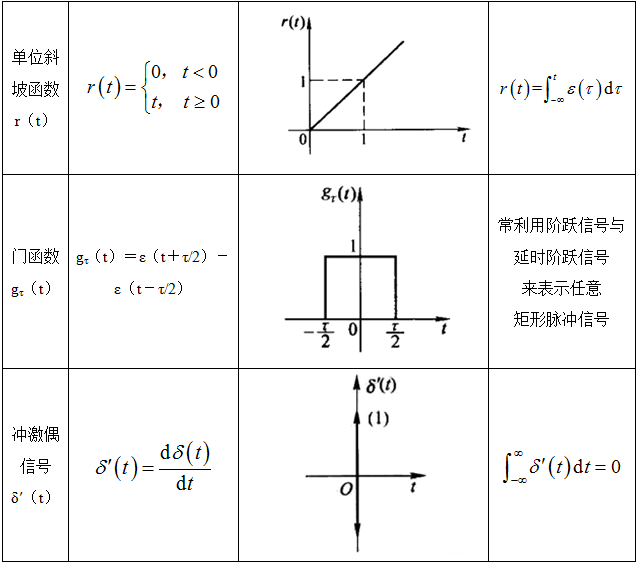
1常用连续信号（见表1-1-3）

表1-1-3 常用连续信号

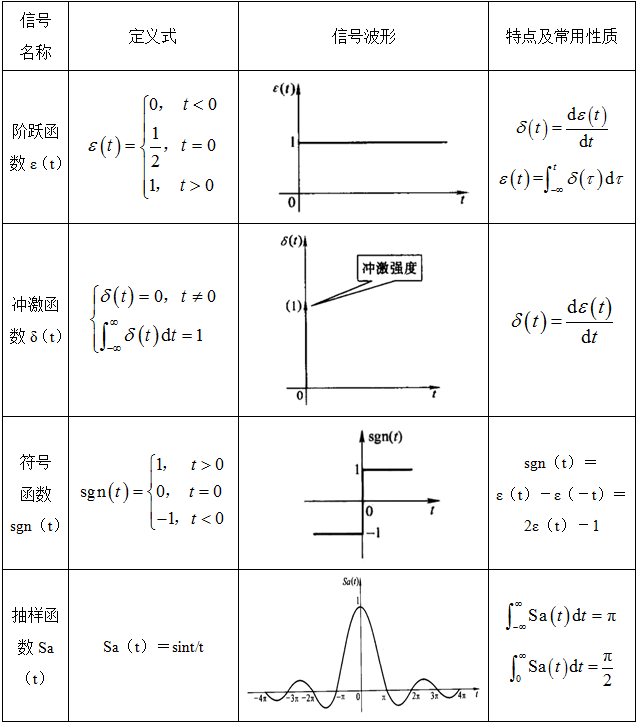
2常用离散信号（见表1-1-4）

表1-1-4 常用离散信号

3冲激函数的基本性质（见表1-1-5）

表1-1-5 冲激函数的基本性质

四、系统的定义、分类及描述

1系统的定义

系统是由若干相互关联的单元组合而成的具有某种功能以用来达到某些特定目的的有机整体，此为系统广义的定义。对电信号而言，系统可看作是对信号进行存储、转换、传输和处理的物理装置。

2系统的分类

①连续时间系统和离散时间系统。

②即时系统和动态系统。

③无源系统和有源系统。

④集总参数系统和分布系统。

⑤线性系统与非线性系统。

⑥时变系统与时不变系统。

⑦因果系统与非因果系统。

⑧稳定系统与非稳定系统。

3系统描述

（1）系统的数学模型：

系统的数学模型是系统物理特性的抽象，是以数学表达式来表征系统的特性。描述连续系统的数学模型是微分方程，而描述离散系统的数学模型是差分方程。

（2）系统的框图表示：

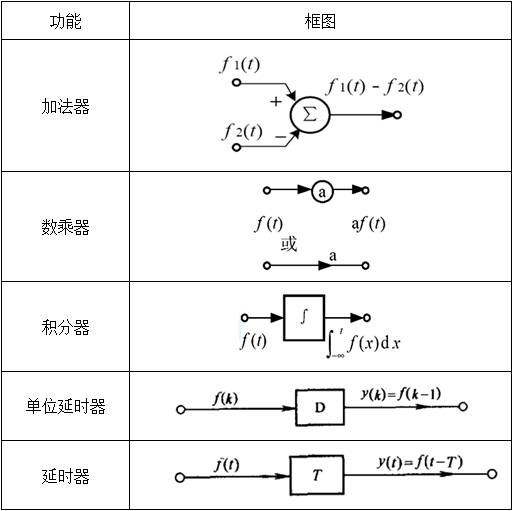
将基本运算（相乘、微分、相加运算）用一些理想部件符号表示出来并相互联接表征上述方程的运算关系，这样画出的图称为模拟框图，简称框图，系统的基本单元框图见表1-1-6。

表1-1-6 系统基本单元框图

五、系统特性

1线性

系统的激励f（t）所引起的响应y（t），可简记为y（t）＝T［f（t）］。线性是指系统同时具备齐次性和可加性。

（1）齐次性：若系统的激励f（t）增大a倍，其响应y（t）也增大a倍，即T［af（t）］＝aT［f（t）］。则称该系统是齐次的。

（2）可加性：若系统的激励之和的响应等于各个激励所引起的响应之和，即T［f₁（t）＋f₂（t）］＝T［f₁（t）］＋T［f₂（t）］。

若系统既是齐次的又是可加的，则称该系统是线性的，即T［af₁（t）＋bf₂（t）］＝aT［f₁（t）］＋bT［f₂（t）］。

2时不变性

时不变性表现为系统响应的形状不随激励施加的时间不同而改变。即，若T［{0}，f（t）］＝y_zs（t），有T［{0}，f（t－t_d）］＝y_zs（t－t_d）。

3因果性

因果性是指系统的响应不应出现在激励之前，只对自变量是时间的系统有意义。若x（t）＝0，t＜t₀。即因果系统的输出不会出现在输入之前。许多以时间为自变量的实际系统都是因果系统，如收音机、电视机、数据采集系统等。

4稳定性

稳定性是指对于有界的输入，系统的输出也是有界的。称为有界输入有界输出（BIBO）稳定系统；否则不稳定。若系统的激励|f（t）|＜∞时，其零状态响应|y_zs（t）|＜∞，则称该系统是稳定的。

六、线性时不变（LTI）系统

若系统既满足线性性质，又满足时不变特性，则称该系统为线性时不变系统，简称为LTI系统。

LTI系统满足微分性和积分性：若f（t）→y_zs（t），则

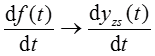
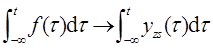
 完整版链接：/Ebook/992800.html

【目录】达聪学习网“吴大正《信号与线性系统分析》第4版教材讲义课后答案”