奥本海姆信号与系统第2版复习笔记电子书

奥本海姆《信号与系统》（第2版）考点知识总结

第7章 采样【复习笔记】

本章重点介绍了采样和采样定理，采样定理在连续时间信号和离散时间信号之间起着桥梁作用，采样在利用离散时间系统技术来实现连续时间系统并处理连续时间信号方面有着至关重要的作用。学完本章读者应该掌握以下内容：

（1）重点掌握采样的过程和采样定理，牢记奈奎斯特采样频率。

（2）掌握内插的定义及如何利用内插由样本重建信号。

（3）重点掌握连续时间信号的离散时间化处理过程。

（4）了解数字微分器及其频率特性。

（5）掌握离散时间信号采样的原理及恢复原离散时间信号的方法。

一、用信号样本表示连续时间信号：采样定理

1冲激串采样

（1）冲激串采样的定义

冲激串采样是指用一个周期冲激串p（t）去乘待采样的连续时间信号x（t）。该周期冲激串p（t）称为采样函数，周期T称为采样周期，而p（t）的基波频率ω＝2π/T称为采样频率。

（2）冲激串采样过程（见图7-1-1）

在时域中有

x_p（t）＝x（t）p（t）

在频域中有

即X_p（jω）是频率ω的周期函数，它由一组移位的X（jω）的叠加组成，但在幅度上标以1/T的变化。

图7-1-1 冲激串采样过程

（3）采样定理

频带宽度有限信号x（t），在|ω|＞ω_M时，X（jω）＝0。如果ω_s＞2ω_M，其中ω_s＝2π/T，那么x（t）唯一地由其样本x（nT），n＝0，±1，±2，…，所确定。其中频率2ω_M称为奈奎斯特率。

已知这些样本值，重建x（t）的办法：

①产生一个冲激幅度就是这些依次而来的样本值的周期冲激串。

②将该冲激串通过一个增益为T，截止频率大于ω_M而小于ω_s－ω_M的理想低通滤波器，该滤波器的输出就是x（t）。

2零阶保持采样

（1）零阶保持的含义

在一个给定的瞬时对x（t）采样并保持这一样本值，直到下一个样本被采到为止，利用零阶保持采样的原理图如图7-1-2所示。

图7-1-2 利用零阶保持采样

（2）零阶保持采样的过程

零阶保持的输出x₀（t）在原理上可以用冲激串采样，再紧跟着一个线性时不变系统（该系统具有矩形的单位冲激响应）来得到，如图7-1-3所示。

①用一个单位冲激响应为h_r（t），频率响应为H_r（jω）的线性时不变系统来处理x₀（t）。

②给出一个H_r（jω），以使r（t）＝x（t）。

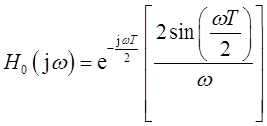
这就要求

若H_r（jω）的截止频率等于ω_s/2，则紧跟在一个零阶保持系统后面的重建滤波器的理想模和相位特性如图7-1-4所示。零阶保持输出本身就被认为是一种对原始信号的充分近似，用不着附加任何低通滤波。

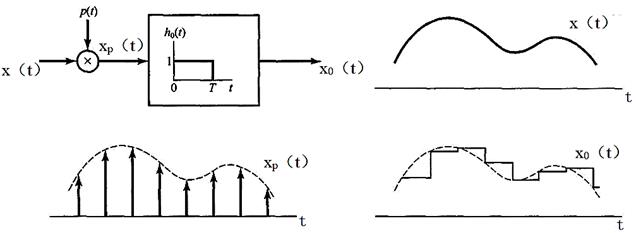
图7-1-3 零阶保持输出x₀（t）的原理图

图7-1-4 为零阶保持采样重建信号的重建滤波器的模和相位特性

需要注意以下两点：①零阶保持输出本身就被认为是一种对原始信号的充分近似，而不用附加任何低通滤波；②H_r（jω）不可能真正实现，必须进行充分近似设计。

二、利用内插由样本重建信号

内插是一个由样本值来重建某一函数的常用过程，也就是用一连续信号对某一组样本值的拟合。

1零阶保持

零阶保持可以看成在样本之间进行内插的一种形式，图7-1-5是零阶保持和理想内插滤波器的传输函数。

图7-1-5 零阶保持和理想内插滤波器的传输函数

2线性内插（一阶保持）

（1）线性内插是将相邻的样本点用直线直接连起来，如图7-1-6所示。

图7-1-6 线性内插（虚线表示原始信号，实线表示线性内插）

（2）利用理想低通滤波器的单位冲激响应的内插（即带限内插）

①输入x_r（t）＝x_p（t）*h（t）时

上式体现了在样本点x（nT）之间如何拟合成一条连续曲线，因此代表了一种内插公式。

②对于理想低通滤波器H（jω），h（t）为

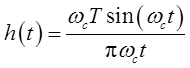
所以有

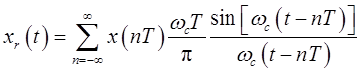
按照上式在ω_c＝ω_s/2时的重建过程如图7-1-7所示，其中（a）图表示带限信号x（t），（b）图表示x（t）的样本冲激串；（c）图表示用sinc函数的叠加取代冲激串的理想带限内插。

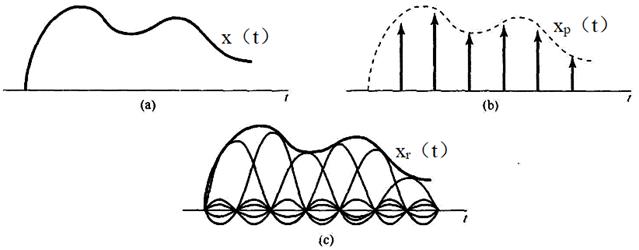
图7-1-7 利用sinc函数的理想带限内插

3高阶保持

零阶保持是一种很粗糙的近似，高阶保持是更为平滑的内插手段，它们所产生的恢复信号具有更好的平滑度。

三、欠采样的效果：混叠现象

混叠是指采样后信号的频谱发生重叠导致失真的现象。即当ω_s＜2ω_M时，x（t）的频谱X（jω）不在X₀（jω）中重复，因此利用低通滤波不能把x（t）从采样信号中恢复出来，这时单项发生重叠，被重建的信号x_r（t）不等于x（t）。

需要注意：采样定理明确要求采样频率大于信号中最高频率的2倍，而不是大于或等于最高频率的2倍。

内容来源

奥本海姆《信号与系统》第2版笔记和课后习题详解

扫码阅读

四、连续时间信号的离散时间处理

1对连续时间信号的处理方法

处理方法分为以下三个过程，框图如图7-1-8所示。

（1）连续时间到离散时间的转换（C/D）：x_d[n]＝x_c（nT）。

（2）离散时间系统内部处理，x_d[n]和y_d[n]都是对应于x_c（t）和y_c（t）的离散时间信号。

（3）离散时间到连续时间的转换（D/C），实现的是作为它的输入的各样本点之间的内插。

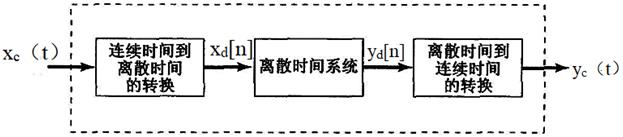
图7-1-8 连续时间信号的离散时间处理

2连续时间信号

x_c（t）和它的离散时间表示x_d[n]之间的关系。

把从连续时间到离散时间的变换表示成一个周期采样的过程，再紧跟着一个把冲激串映射为一个序列的环节，整个系统的表示如图7-1-9所示，其中图（a）表示整个系统；图（b）表示两种采样率的x_p（t），虚线包络代表x_c（t）；图（c）表示两种不同采样率的输出序列。

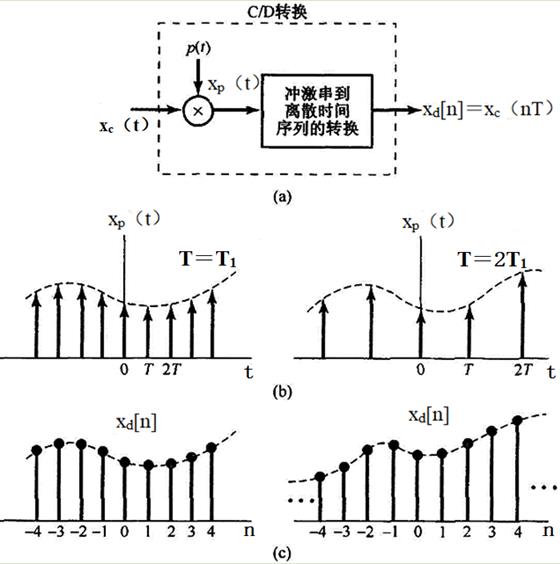
图7-1-9 用一个周期冲激串采样，再跟着一个到离散时间序列的转换

需要注意：连续时间的频率变量用ω表示，将离散时间的频率变量用Ω表示。

3X_c（jω）、X_p（jω）和X_d（e^jΩ）的关系

x_c（t）和y_c（t）的连续时间傅里叶变换分别用X_c（jω）和Y_c（jω）表示；而x_d[n]和y_d[n]的离散时间傅里叶变换分别用X_d（e^jΩ）和Y_d（e^jΩ）表示。

（1）用x_c（t）的样本值来表示x_p（t）的连续时间傅里叶变换X_p（jω）

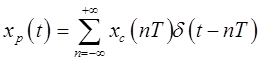
又δ（t－nT）的傅里叶变换是e^－jωnT，所以

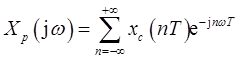
现在考虑x_d[n]的离散时间傅里叶变换，即

因为x_d[n]＝x_c（nT），因此

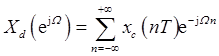
从而可得X_d（e^jΩ）和X_p（jω）的关系

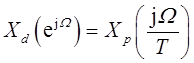
又因为

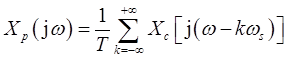
因此得到

（2）X_c（jω）、X_p（jω）和X_d（e^jΩ）三者之间的关系（见图7-1-10）

①X_d（e^jΩ）是X_p（jω）的重复，唯频率坐标有一个尺度变换。

②x_d[n]和x_r（t）之间的频谱关系，是通过先把x_c（t）的频谱X_c（jω）按

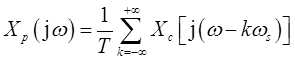
进行周期重复，然后再跟着一个按

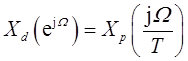
的线性频率尺度变换联系起来的。

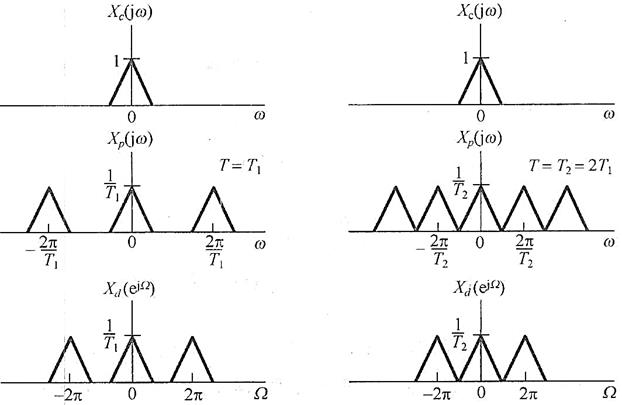
图7-1-10 在两种不同采样率下，X_c（jω）、X_p（jω）和X_d（e^jΩ）之间的关系

4利用离散时间滤波器过滤连续时间信号的系统（见图7-1-11）

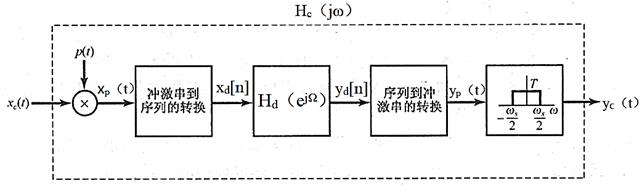
图7-1-11 利用离散时间滤波器过滤连续时间信号的系统

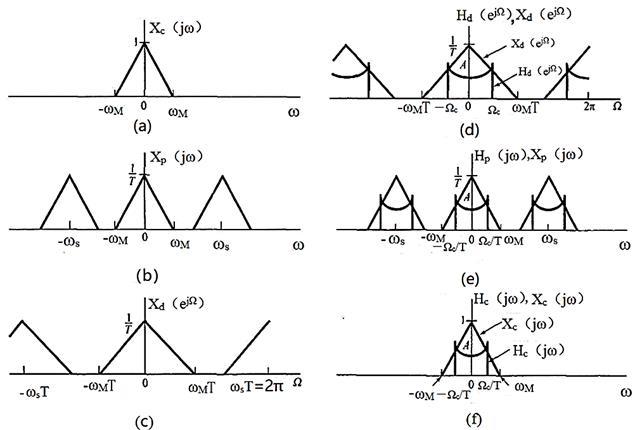
图7-1-12 图7-1-11所示系统的频域说明

其中（a）连续时间信号的频谱X_c（jω）；（b）冲激串采样以后的谱；（c）离散时间序列x_d[n]的谱；（d）H_d（e^jΩ）和X_d（e^jΩ）相乘后得到的Y_d（e^jΩ）；（e）H_p（jω）和X_p（jω）相乘后得到的Y_P（jω）；（f）H_c（jω）和X_c（jω）相乘后得到的Y_c（jω）。

（1）图7-1-12左边是某一代表性的频谱X_c（jω）、X_p（jω）和X_d（e^jΩ），其中假定ω_M＜ω_s/2，所以没有混叠发生。相应于时间滤波器输出的谱Y_d（e^jΩ）是X_d（e^jΩ）和H_d（e^jΩ）相乘，如图7-1-12（d）所示。

（2）变换到Y_c（jω）就相应于进行频率尺度的变换，然后进行低通滤波，所得到的频谱分别如图7-1-12（e）和图7-1-12（f）所示。

（3）因为Y_d（e^jΩ）是两个互为重叠的频谱积，如图7-1-12（d）所示，所以对两者都应施加频率尺度的变换和滤波。

（4）将图7-1-12（a）和（f）进行比较，可得Y_c（jω）＝X_c（jω）H_d（e^jωT），在输入是充分带限的，并满足采样定理的条件下，图7-1-12的整个系统事实上就等效于一个响应为H_c（jω）的连续时间系统，而H_c（jω）与离散时间频率响应H_d（e^jΩ）的关系为

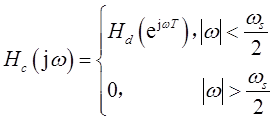
等效的连续时间滤波器的频率响应是该离散时间滤波器在一个周期内的特性，只是频率轴有线性尺度变化。

5数字微分器

……

 完整版链接：/Ebook/993228.html

【目录】达聪学习网“奥本海姆《信号与系统》（第2版下册）复习笔记课后答案”