周世勋量子力学教程第2版课后题答案

周世勋《量子力学教程》第二版第二章课后习题详解

2.1 证明在定态中，概率流密度与时间无关。

解：对于定态波函数有

所以由概率流密度定义公式可得

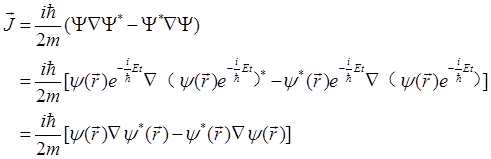
显而易见，J→与t无关。

2.2 由下列两定态波函数计算概率流密度：（1）ψ₁＝（1/r）exp（ikr）；（2）ψ₂＝（1/r）exp（－ikr）。从所得结果说明ψ₁表示向外传播的球面波，ψ₂表示向内（即向原点）传播的球面波。

解：在球坐标中

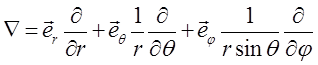
（1）由概率流密度定义公式可得

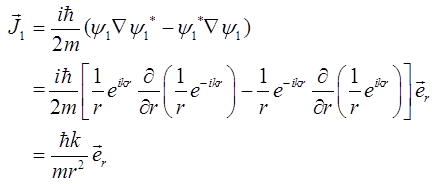
J→₁与r→同向，表示向外传播的球面波。

（2）

可见，J→₂与r→反向，表示向原点传播的球面波。

2.3 一粒子在一维势场中运动，求粒子的能级和对应的波函数。

解：题中U（x）与t无关，所以由定态薛定谔方程即可求解本征值和本征函数

在各区域的具体形式为

Ⅰ：x＜0

ψ₁（x）＝0①

Ⅱ：0≤x≤a

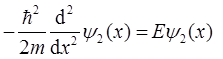②

Ⅲ：x＞a

ψ₃（x）＝0③

方程②可变为

令k²＝2mE/（ħ²），得

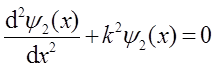
其解为：

ψ₂（x）＝Asinkx＋Bcoskx④

根据波函数的标准条件确定系数A，B，由连续性条件，得

ψ₂（0）＝ψ₁（0）⑤

ψ₂（a）＝ψ₃（a）⑥

则B＝0，进而Asinka＝0。因为A≠0，所以sinka＝0，则ka＝nπ（n＝1，2，3，…），因此

ψ₂（x）＝Asin（nπ/a）x

由归一化条件

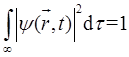
得

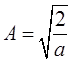
则

本征能量为E_n＝[π²ħ²/（2ma²）]n²（n＝1，2，3，…）

本征波函数为

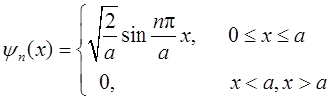
2.4 证明下式中的归一化因子是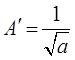

证明：

由归一化，得

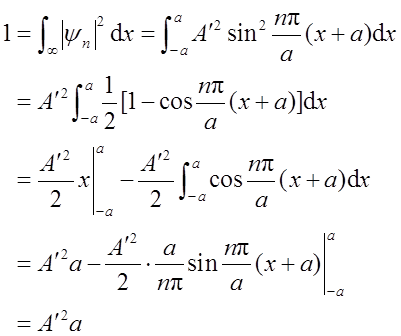
所以归一化常数，为方便起见，可以取α＝0，即得

内容来源

周世勋《量子力学教程》第2版考点笔记课后答案

扫码阅读

2.5 求一维谐振子处在第一激发态时概率最大的位置。

解：

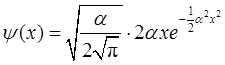
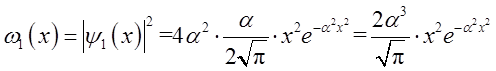
令

得：x＝0，x＝±1/α，x＝±∞。

检验所得数值是否为最大值的位置

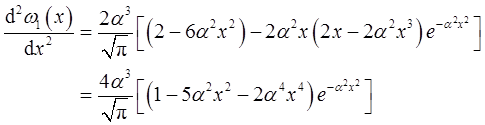
只有x＝±1/2带入的结果为负值。可见是所求几率最大的位置。

2.6 在一维势场中运动的粒子，势能对原点对称：U（－x）＝U（x），证明粒子的定态波函数具有确定的宇称。

解：在一维势场中运动的粒子的定态S-方程为

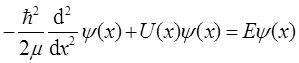①

将式中的x以（－x）代换，d²/dx²不变，由此可得

②

利用U（－x）＝U（x），得

③

所以ψ（－x）＝cψ（x）④

因此由ψ（x）＝cψ（－x）⑤

由④乘⑤得：

ψ（x）ψ（－x）＝c²ψ（x）ψ（－x）

可见，c²＝1，得c＝±1。

因此，当c＝＋1时，ψ（－x）＝ψ（x），则ψ（x）具有偶宇称；当c＝－1时，ψ（－x）＝－ψ（x），则ψ（x）具有奇宇称。

所以当势场满足U（－x）＝U（x）时，粒子的定态波函数具有确定的宇称。

2.7 一粒子在一维势阱中运动。求束缚态（0＜E＜U₀）的能级所满足的方程。

解：粒子所满足的薛定谔方程为

Ⅰ：

Ⅱ：

Ⅲ：

令

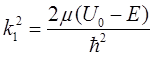
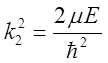
则方程变为

Ⅰ：

Ⅱ：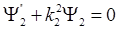

Ⅲ：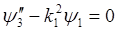

各方程的解为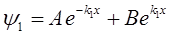：；ψ₂＝Csink₂x＋Dcosk₂x；

由波函数的有限性，有：ψ₁（－∞）有限，则A＝0；ψ₃（∞）有限，则E＝0。因此，，。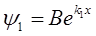

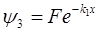再根据波函数及其导函数的连续性，有：ψ₁（－a）＝ψ₂（－a），ψ₂（a）＝ψ₃（a）；ψ₁′（－a）＝ψ₂′（－a），ψ₂′（a）＝ψ₃′（a）。

整理得

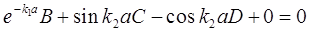
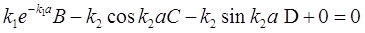
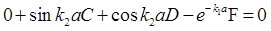
解此方程即可得出B、C、D、F，进而得出波函数的具体形式。要使方程组有非零解，必须

化简得

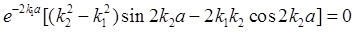
因为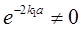，则

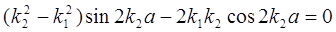
即

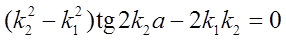
为所求束缚态能级所满足的方程。

【注】本题也可以根据复习笔记中所提到的U（－x）＝U（x）这个特点，把所求的波函数分成满足奇宇称和偶宇称两种情况来讨论，这样能简化求解过程中的繁杂计算。

2.8 分子间的范德瓦耳斯力所产生的势能可以近似地表示为

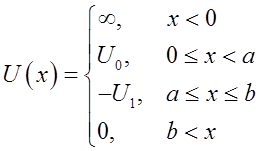
求束缚态的能级所满足的方程。

解：定态薛定谔方程为

Ⅰ：

ψ₁（x）＝0（x＜0）

Ⅱ：

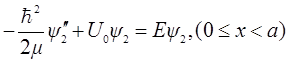
Ⅲ：

Ⅳ：

对于本题势能对应的束缚态来说，有E＜0。

整理可得

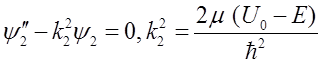
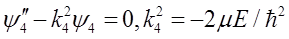
各方程的解分别为：ψ₁＝0；；ψ₃＝Csink₃x＋Dcosk₃x；

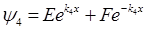
由波函数及其一阶导数的连续性条件得

ψ₂（0）＝ψ₁（0），则A＋B＝0；

ψ₂＝2Asinhk₂x，ψ₄（∞）有限，则E＝0；

ψ₂（a）＝ψ₃（a），则2Asinhk₂a＝Csink₃a＋Dcosk₃a；

ψ₂′（a）＝ψ₃′（a），则2k₂Acoshk₂a＝Ck₃cosk₃a－Dk₃sink₃a；

ψ₃（b）＝ψ₄（b），则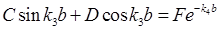

ψ₃′（b）＝ψ₄′（b），则

将上述几个方程看做以A、C、D、F为自变量的四元一次方程组，有非平凡解的条件是系数行列式为0，即应满足

整理得

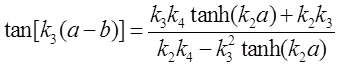
此即为所要求的束缚态能级所满足的方程。

 完整版链接：/Ebook/967980.html

【目录】达聪学习网“量子力学教程第二版复习笔记课后习题答案”