伍德里奇计量经济学导论第6版复习笔记电子书

第2章 简单回归模型

考点一：简单回归模型的定义 ★★

1、简单线性回归模型

假定方程为：y＝β₀＋β₁x＋u，若该方程在总体中成立，则它便定义了一个简单线性回归模型。模型将变量x和y联系起来，u是误差项或干扰项，表示除x之外的影响y的因素。β₀和β₁为待估参数，分别表示截距项和变量x的斜率。

2、零条件均值假定

（1）零条件均值

u的平均值与x值无关且为0，即u的均值独立于x。满足：E（u｜x）＝E（u）＝E（xu）＝Cov（x，u）＝0。

（2）零条件均值假定的意义

①使β₁有了另一种非常有用的解释。以x为条件取y的期望值，可得：E（y｜x）＝β₀＋β₁x。方程表明，总体回归函数（PRF）E（y｜x）是x的线性函数，β₁是斜率参数。对任何给定的x值，y的分布都以E（y｜x）为中心。

②在给定该假定后，把方程中的y看成两个部分是比较有用的。一部分是y的系统部分，即β₀＋β₁x，这是由x解释的部分；另一个部分是非系统部分u，即不能由x解释的那一部分。

考点二：普通最小二乘法 ★★★★★

1、最小二乘估计值

令{（x_i，y_i）：i＝1，…，n}表示从总体中抽取的一个容量为n的随机样本，满足：y_i＝β₀＋β₁x_i＋u_i。第i次的残差是y_i与预期拟合值之差，即：u∧_i＝y_i－y∧_i＝y_i－β∧₀－β∧₁x_i。OLS估计的方法就是要使残差平方和最小，即：

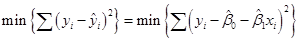
对上式关于β∧₀和β∧₁分别求偏导，得到：

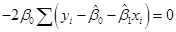
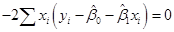
可简写为：∑u∧_i＝0和∑x_iu∧_i＝0。通过求解两个方程即可得到β∧₀和β∧₁为：

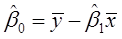
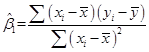
一旦确定了截距和斜率的OLS估计值，就可以建立OLS回归线：y∧＝β∧₀＋β∧₁x，这被称为样本回归函数（SRF），因为它是总体回归函数的一个样本估计。总体回归函数是固定且未知的，而样本回归函数则来自一组给定的数据样本，不同的样本会使方程产生不同的斜率和截距。

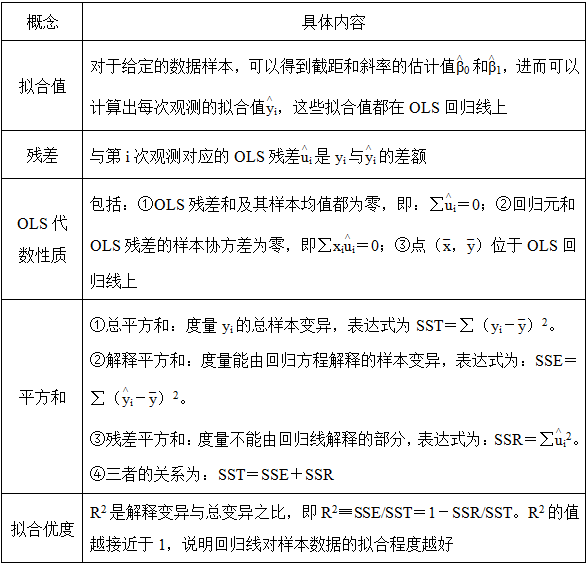
2、简单回归的相关概念（见表2-1）

表2-1 简单回归的相关概念

考点三：度量单位和函数形式 ★★★★

1、改变度量单位对OLS统计量的影响

（1）当改变因变量的度量单位时，很容易计算出截距和斜率估计值的变化。若因变量乘以一个常数c，则截距和斜率的OLS估计值都将扩大为原来的c倍。

（2）若将自变量除以或乘以一个非零常数c，则OLS斜率系数也应分别被乘以或除以c。

（3）一般地，如果只改变自变量的度量单位，截距估计值是不会变化的。

（4）模型的拟合优度值与变量的度量单位无关。

2、在简单回归中加入非线性因素

百分比影响（近似）为常数的模型形式为：logy＝β₀＋β₁x＋u。特别地，若∆u＝0，有：%∆y≈（100·β₁）∆x。

常弹性模型是自然对数的另一个应用，形式为：logy＝β₀＋β₁logx＋u。若令y＝logy，x＝logx，则这个模型就变为了简单回归模型。斜率参数β₁表示x关于y的弹性。

3、含对数的函数的几种形式（见表2-2）

表2-2 含对数的函数的几种形式

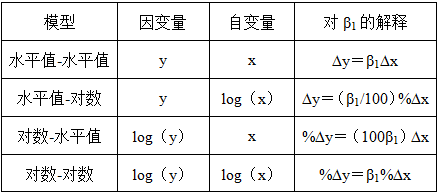
4、“线性”回归的含义

“线性”的含义是指相对于参数而言模型是线性的，即方程中的参数β₀和β₁是线性形式的，而被解释变量和解释变量的形式可以是线性也可以是非线性的。

考点四：OLS估计量的期望值和方差 ★★★★★

1、OLS的无偏性

（1）相关假定（见表2-3）

表2-3 相关假定

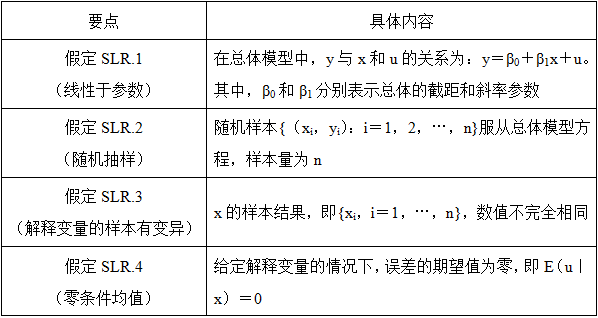
（2）β∧₁与β₁的差异

已知斜率估计量为：

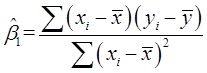
将y_i＝β₀＋β₁x_i＋u_i代入上式的分子中，分子变为：

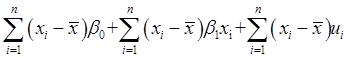
又因为：

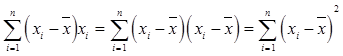
故斜率估计量可变为：

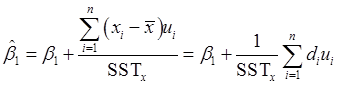
其中：d_i＝x_i－x＿。上式说明，β∧₁等于β₁加上误差的一个线性组合。由于误差一般都不为零，所以β∧₁与β₁存在差异。

（3）OLS的无偏性

利用假定SLR.1～SLR.4，对于任意的β₀和β₁，有E（β∧₀）＝β₀与E（β∧₁）＝β₁成立，即β∧₀与β∧₁具有无偏性。

证明如下：

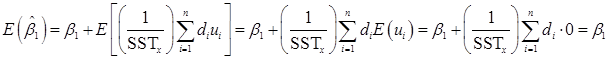
此外，对于β∧₀，有：β∧₀＝y＿－β∧₁x＿＝β₀＋β₁x＿＋u＿－β∧₁x＿＝β₀＋（β₁－β∧₁）x＿＋u＿。因为E（u＿）＝0，故以x_i的值为条件，有：E（β∧₀）＝β₀＋E[（β₁－β∧₁）x＿]＋E（u＿）＝β₀＋E[（β₁－β∧₁）x＿]。又因为E（β∧₁）＝β₁，所以E（β∧₀）＝β₀。

2、OLS估计量的方差

（1）相关假定

假定SLR.5（同方差性）：在给定解释变量时，误差的方差都相同，即Var（u｜x）＝σ²。

（2）OLS估计量的抽样方差

在假定SLR.1～SLR.5下，以样本值{x₁，x₂，…，x_n}为条件，有：

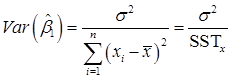
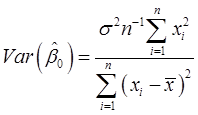
内容来源

伍德里奇《计量经济学导论》第6版复习笔记课后答案

扫码阅读

3、误差方差的估计

（1）误差与残差的区分

利用随机样本观测将总体模型写为：y_i＝β₀＋β₁x_i＋u_i。还可以将y_i用其拟合值和残差表示出来：y_i＝β∧₀＋β∧₁x_i＋u∧_i。比较这两个方程可以发现，误差出现在包含总体参数β₀和β₁的方程中，残差则出现在包含估计值β∧₀和β∧₁的估计方程中。由于总体参数未知，所以误差无法观测；但残差是可以根据数据计算得到的。

因为：u∧_i＝y_i－β∧₀－β∧₁x_i＝（β₀＋β₁x_i＋u_i）－β∧₀－β∧₁x_i＝u_i－（β∧₀－β₀）－（β∧₁－β₁）x_i，且β∧₀与β∧₁具有无偏性，所以二者之差的期望值为零。

（2）σ²的无偏估计量

对自由度进行调整，可以得到σ²的无偏估计量为：

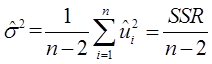
（3）σ²的无偏估计

在假定SLR.1～SLR.5下，有：E（σ∧²）＝σ²。

证明：将u∧_i＝u_i－（β∧₀－β₀）－（β∧₁－β₁）x_i关于所有i进行平均，有：0＝u＿－（β∧₀－β₀）－（β∧₁－β₁）x＿。从原方程中减去它，可得：u∧_i＝（u_i－u＿）－（β∧₁－β₁）（x_i－x＿）。所以：u∧_i²＝（u_i－u＿）²＋（β∧₁－β₁）²（x_i－x＿）²－2（u_i－u＿）（β∧₁－β₁）（x_i－x＿）。对所有i求和，又得到：

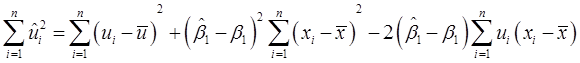
对上式取期望值，有：

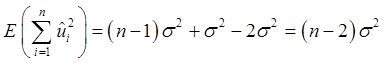
因此：E[SSR/（n－2）]＝σ²。σ的自然估计量为：

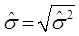
上式也称为回归标准误差（SER）。尽管σ∧不具有无偏性，但具有一致性。β∧₁的标准误差为：

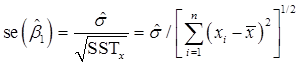
 完整版链接：http://dacai.100xuexi.com/Ebook/990740.html

【目录】达聪学习网“伍德里奇《计量经济学导论》第六版教材讲义课后习题答案”