孟道骥《高等代数与解析几何》第3版课后习题详解
孟道骥《高等代数与解析几何》(第3版)课后习题详解
解析课后习题,提供详尽答案。本书参考了该教材的国内外配套资料和其他教材的相关知识对该教材的课(章)后习题进行了详细的分析和解答,并对相关重要知识点进行了延伸和归纳。
立即阅读 >>
孟道骥《高等代数与解析几何》(第3版)课后习题详解 【完整内容点击文中链接获取】
第1章 多项式
第1节 数域
1、举出对加法、乘法及除法封闭但对减法不封闭的例子。
解:集合Q+={a∈Q|a>0}对加法、乘法及除法封闭但是对减法不封闭。
2、举出对加法、减法封闭,但对乘法不封闭的例子。
解:集合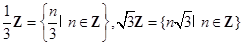 对加法、减法都封闭,但是对乘法不封闭。
对加法、减法都封闭,但是对乘法不封闭。
3、举出对加法、减法都不封闭,但对乘法封闭的例子。
解:集合S={2n|n∈N},{1},{2m+1|m∈Z}与集合{m|p∤m,p素数}对加法、减法都是不封闭的,但是对乘法封闭。
4、试证C的子集P若对减法封闭,则必对加法封闭。
证明:可设P≠∅,于是有a∈P,因此a-a=0∈P。又因为0-a=-a∈P,若有b∈P,则必有a+b=b+a=b-(-a)∈P。故P若对减法封闭,则必对加法封闭。
5、试证C的子集P若对除法封闭,则必对乘法封闭。
证明:设P≠∅,P≠{0},于是有a∈P,a≠0,因此a÷a=1∈P。又因为1÷a=a-1∈P,故若b∈P成立,则有ab=ba=b÷a-1∈P。因此P若对除法封闭,则必对乘法封闭。
6、令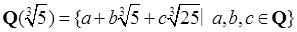
试证明![]() 是一个数域。
是一个数域。
证明:由题目易知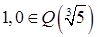 ,若
,若
则有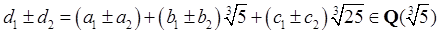
即![]() 对加法和减法都封闭。又因为
对加法和减法都封闭。又因为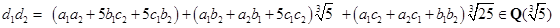
则![]() 对乘法封闭。
对乘法封闭。
下面需证明![]() 对除法是封闭的。由于对乘法封闭,故只需证明下面结论:
对除法是封闭的。由于对乘法封闭,故只需证明下面结论:
若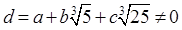
则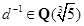 成立。
成立。
下面分为三种情形讨论:
(1)b=c=0,此时d=a≠0,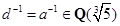 。
。
(2)c=0,b≠0,此时可设 ,于是
,于是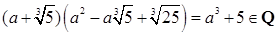
且a3+5≠0。因此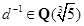 。
。
(3)c≠0,此时可设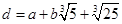 ,于是
,于是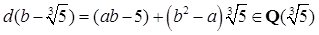
因此有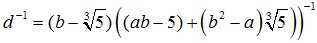
由情形(2)及乘法的封闭性可知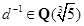 。故
。故![]() 是数域。
是数域。
| 内容来源 | 孟道骥《高等代数与解析几何》(第3版)课后习题详解  |
第2节 一元多项式
1、设P是数域。f(x),g(x),h(x)∈P[x],且f(x)+g(x)=f(x)+h(x)。试证g(x)=h(x)。
证明:由题意知f(x)+g(x)=f(x)+h(x),于是有
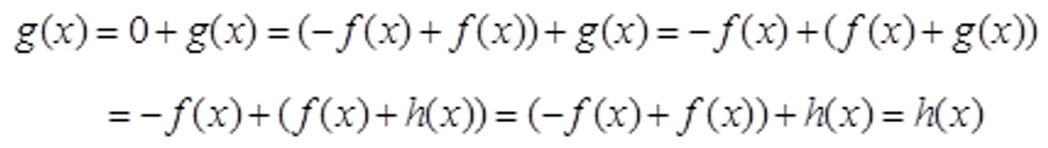
故结论成立。
2、设f(x),g(x),h(x)∈P[x],且f(x)≠0,f(x)g(x)=f(x)h(x)。试证g(x)=h(x)。
证明:由题意有f(x)g(x)=f(x)h(x),则f(x)(g(x)-h(x))=0,再由f(x)≠0,因此结论成立。
3、设f(x),g(x)∈P[x],f(x)≠0,g(x)≠0,又deg(f(x)g(x))=degg(x)。试证f(x)=c∈P。
证明:因为degf(x)+degg(x)=deg(f(x)g(x))=degg(x),所以degf(x)=0,故f(x)=c∈P。
4设m,n∈N,f(x)∈P[x]。归纳定义f1(x)=(f(x))1=f(x),fn(x)=(f(x))n=f(x)fn-1(x),试证
1)fn(x)fm(x)=fm+n(x);
2)(fn(x))m=fmn(x);
3)(f(x)g(x))n=fn(x)gn(x);
4)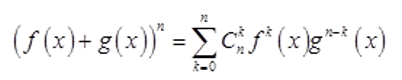
这里f0(x),g0(x)定义为1。
证明:1)对m,n作双重归纳证明。由fn(x)的定义,可知对任何m有f(x)fm(x)=f1+m(x)。现设对于n,有fn(x)fm(x)=fn+m(x)成立,则
fn+1(x)fm(x)=(f(x)fn(x))fm(x)=f(x)(fn(x)fm(x))=f(x)fn+m(x)=fn+1+m(x)
因此结论1)成立。
2)当m=1时,结论显然成立。设m时,结论成立,于是由结论1)有
(fn(x))m+1=fn(x)(fn(x))m=fn(x)fmn(x)=fn+mn(x)=fn(m+1)(x)
则结论2)成立。
3)n=1时,结论显然成立。设n时,结论成立,于是有
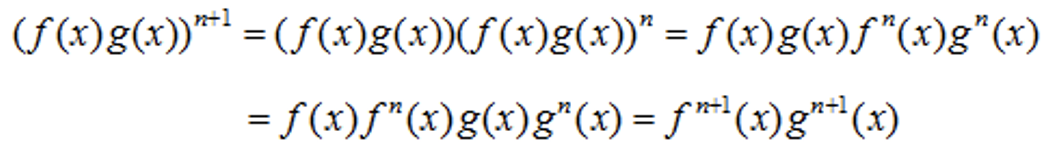
因此结论3)成立。
4)n=1时,结论显然成立。设n时,结论成立,于是有

因此结论4)成立。
……
【完整版】 达聪网 孟道骥《高等代数与解析几何》(第3版)课后习题详解
热门内容
茆诗松《概率论与数理统计教程》(第3版)全套资料【笔记+题库】
胡运权《运筹学教程》(第5版)配套题库【考研真题精选+课后习题+章节题库】



共有 0 条评论