工程数学线性代数同济大学第6版复习笔记
达聪学习网帮助同学们备考提供以下配套复习资料,希望能帮助大家快速巩固知识点,轻松上岸。
★资料名称:同济大学数学系《工程数学—线性代数》(第6版)笔记和课后习题(含考研真题)详解
资料链接:https://dacai.100xuexi.com/EBook/1002356.html
第1章 行列式
1.1 复习笔记
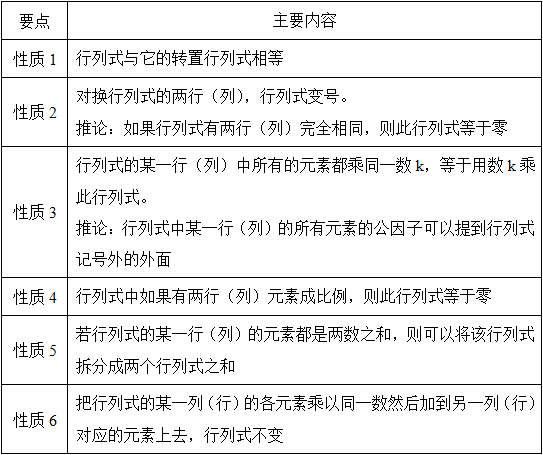
一、行列式的性质(见表1-1)
表1-1 行列式的性质
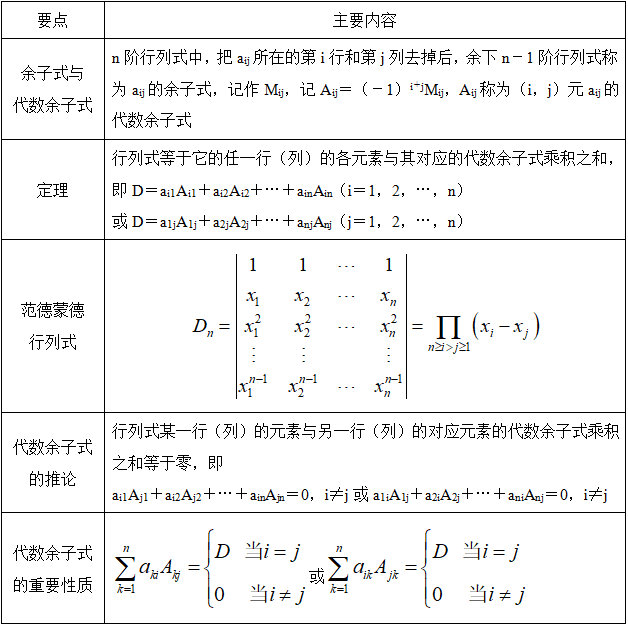
二、行列式按行(列)展开(见表1-2)
表1-2 行列式按行(列)展开
1.2 课后习题详解
1利用对角线法则计算下列三阶行列式:
(1) ;
;
(2)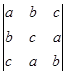 ;
;
(3)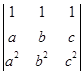 ;
;
(4)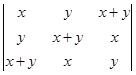 。
。
解:(1)原式=2×(-4)×3+0×(-1)×(-1)+1×1×8-1×(-4)×(-1)-2×(-1)×8-0×1×3=-4。
(2)原式=acb+bac+cba-c3-a3-b3=3abc-a3-b3-c3。
(3)原式=1·b·c2+1·c·a2+1·a·b2-1·b·a2-1·c·b2-1·a·c2=bc2+ca2+ab2-ba2-cb2-ac2=c2(b-a)+ab(b-a)-c(b2-a2)=(a-b)(b-c)(c-a)。
(4)原式=x(x+y)y+yx(x+y)+(x+y)yx-(x+y)3-x3-y3=-2(x3+y3)。
2按自然数从小到大为标准次序,求下列各排列的逆序数:
(1)1 2 3 4;
(2)4 1 3 2;
(3)3 4 2 1;
(4)2 4 1 3;
(5)13…(2n-1)24…(2n);
(6)13…(2n-1)(2n)(2n-2)…2。
解:(1)该排列为标准排列,所以其逆序数为0。
(2)该排列的首位元素4的逆序数为0,第2位元素1的逆序数为1,第3位元素3的逆序数为1,末位元素2的逆序数为2,所以其逆序数为:0+1+1+2=4。
(3)该排列的前两位元素的逆序数均为0,第3位元素2的逆序数为2;末位元素1的逆序数为3,所以其逆序数为:0+0+2+3=5。
(4)该排列的从首位元素到末位元素的逆序数依次为0,0,2,1,所以其逆序数为:0+0+2+1=3。
(5)该排列中前n位元素的逆序数均为0,第n+1位元素2与它前面的n-1个数构成逆序对,所以它的逆序数为n-1;同理可知,第n+2位元素4的逆序数为n-2……末位元素2n的逆序数为0,因此该排列的逆序数为:(n-1)+(n-2)+…+0=n(n-1)/2。
(6)该排列的前n+1位元素的逆序数均为0;第n+2位元素(2n-2)的逆序数为2;第n+3位元素2n-4与它前面的2n-3,2n-1,2n,2n-2构成逆序对,所以它的逆序为4,……,末位元素2的逆序数为2(n-1),因此该排列的逆序数为:2+4+…+2(n-1)=n(n-1)。
《工程数学—线性代数》复习资料  |
1、同济大学数学系《工程数学—线性代数》(第6版)笔记和课后习题(含考研真题)详解
2、同济大学数学系《工程数学—线性代数》(第6版)配套题库【考研真题精选+章节题库】




共有 0 条评论