蒋中一数理经济学的基本方法第4版课后练习题答案

蒋中一数理经济学的基本方法第4版课后答案

第2章 经济模型

1、用集合符号写出下列集合：（a）大于34的所有实数集；（b）大于8但小于65的所有实数集。

答：（a）大于34的所有实数集可以表示为：A＝{x|x＞34}。

（b）大于8但小于65的所有实数集可以表示为：A＝{x|8＜x＜65}。

2、给定集合S₁＝{2，4，6}，S₂＝{7，2，6}，S₃＝{4，2，6}，S₄＝{2，4}，下面哪些说法正确？

（a）S₁＝S₃；（b）S₁＝R；（c）8∈S₂；（d）3∉S₂；（e）4∉S₃；（f）S₄⊂R；（g）S₁⊃S₄；（h）∅⊂S₂；（i）S₃⊃{1，2}。

答：（a）（d）（f）（g）（h）是正确的。（b）应为S₁⊂R，（c）应为8∉S₂，（e）应为4∈S₃，（i）应为{1，2}⊄S₃。

3、根据上题给出的四个集合，求：

（a）S₁∪S₂；

（b）S₁∪S₃；

（c）S₂∩S₃；

（d）S₂∩S₄；

（e）S₄∩S₂∩S₁；

（f）S₃∪S₁∪S₄。

答：（a）S₁∪S₂＝{2，4，6，7}。

（b）S₁∪S₃＝{2，4，6}。

（c）S₂∩S₃＝{2，6}。

（d）S₂∩S₄＝{2}。

（e）S₄∩S₂∩S₁＝{2}。

（f）S₃∪S₁∪S₄＝{2，4，6}。

4、下述哪些说法是正确的？

（a）A∪A＝A；（b）A∩A＝A；（c）A∪∅＝A；（d）A∪U＝U；（e）A∩∅＝∅；（f）A∩U＝A；（g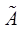）的补集是A。

答：（a）（b）（c）（d）（e）（f）（g）都是正确的。

5、已知集合A＝{4，5，6}，B＝{3，4，6，7}，C＝{2，3，6}，验证分配律。

证明：首先验证A∪（B∩C）＝（A∪B）∩（A∪C），有：

A∪（B∩C）＝{4，5，6}∪{3，6}＝{3，4，5，6}

（A∪B）∩（A∪C）＝{3，4，5，6，7}∩{2，3，4，5，6}＝{3，4，5，6}

所以A∪（B∩C）＝（A∪B）∩（A∪C）成立。

然后验证A∩（B∪C）＝（A∩B）∪（A∩C），则有：

A∩（B∪C）＝{4，5，6}∩{2，3，4，6，7}＝{4，6}

（A∩B）∪（A∩C）＝{4，6}∪{6}＝{4，6}

所以A∩（B∪C）＝（A∩B）∪（A∩C）成立。

综上，分配律得证。

内容来源

蒋中一《数理经济学的基本方法》第4版课后答案

扫码阅读

6、用维恩图法，根据逐次形成阴影的不同顺序，验证分配律。

答：首先验证A∪（B∩C）＝（A∪B）∩（A∪C）。

（B∩C）可以表示为：

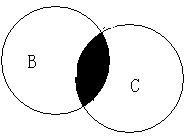
A∪（B∩C）可以表示为：

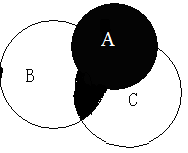
（A∪B）可以表示为：

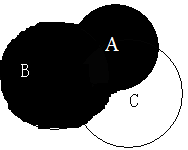
（A∪C）可以表示为：

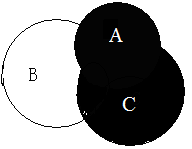
（A∪B）∩（A∪C）可以表示为：

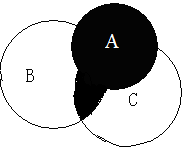
所以A∪（B∩C）＝（A∪B）∩（A∪C）成立。

然后验证A∩（B∪C）＝（A∩B）∪（A∩C）。

（B∪C）可以表示为：

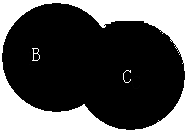
A∩（B∪C）可以表示为：

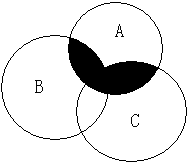
（A∩B）可以表示为：

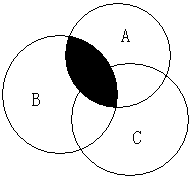
（A∩C）可以表示为：

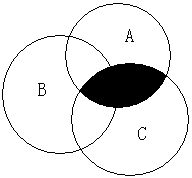
（A∩B）∪（A∩C）：

所以，A∩（B∪C）＝（A∩B）∪（A∩C）成立。

综上，分配律得证。

7、列举集合{5，6，7}的所有子集。

答：{5，6，7}的所有子集为：∅、{5}、{6}、{7}、{5，6}、{5，7}、{6，7}、{5，6，7}。

注：集合包含n个元素，其子集数为2ⁿ。

8、列举集合S＝{a，b，c，d}的所有子集。共有多少个？

答：S＝{a，b，c，d}的所有子集为：∅、{a}、{b}、{c}、{d}、{a，b}、{a，c}、{a，d}、{b，c}、{b，d}、{c，d}、{a，b，c}、{a，b，d}、{a，c，d}、{b，c，d}、{a，b，c，d}。共有16个子集。

9、例6表明∅是U的补集，但因空集是任意集合的子集，所以它必定是U的子集。因为“U的补集”这个术语具有“不在U中”的含义，而“U的子集”这一术语又有“包含在U中”的含义。∅同时具有这两种含义，似乎是自相矛盾的，你如何解释这个谜？

答：全集U的补集为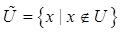，该术语的含义“不在U中”是通过符合“∉”来表示的，而∉表示的是个别元素（x）和集合（U）之间的关系。相反，∅是U的子集，即“空集包含在U中”是通过符合“⊂”表示的，其表示子集（∅）与集合（U）之间的关系。因此，∅必然同时具有两种含义，二者并不矛盾。

……

 完整版链接： /Ebook/965470.html

【推荐】达聪学习网“蒋中一《数理经济学的基本方法》第4版课后习题答案”