胡运权《运筹学教程》第5版配套题库【考研真题精选＋课后习题＋章节题库】

胡运权《运筹学教程》第5版课后习题答案详解【完整内容点击文中链接获取】

第十四章 运筹学中的启发式方法

1、什么是启发式方法？试说明用启发式方法解决实际问题的过程和步骤。

解：（1）启发式方法是指对于结构不良问题，为得到近似可用的解，分析人员必须运用自己的感知和洞察力，从与其有关而较基本的模型与算法中寻求其间的联系，从中得到启发，去发现适于解决该问题的思路和途径的方法。

（2）用启发式方法解决实际问题的过程和步骤：①系统观察和分析实际问题；②抽象并明确提出问题；③建立启发式数学模型；④选择启发式策略，设计启发式方法，按照一定的搜索规则反复迭代逼近模型最优可行解，直到得到满意解；⑤检验和修正模型及其满意解。

2、在解决实际问题时如何运用启发式策略？除书上列出的几个启发式策略之外，你认为还有什么样的有用策略？

解：（1）在解决实际问题时，可根据实际问题的性质和要求来选用某一启发式策略；为得到理想效果，也可将几个策略联合起来使用。

（2）除本书上列出的几个启发式策略之外，还有计算机仿真、模拟策略、类比策略、近似策略等可以使用。

3、对在多台设备上加工多个工件的工件排序问题来说，你认为应如何衡量不同排序方案的优劣？需考虑哪些准则？这些准则的适用条件如何？并举出两个实例加以详细说明。

解：（1）应根据工期最短、成本最低、质量最优等优劣标准来衡量不同排序方案的优劣。

（2）设备充分利用、总加工时间最短等某一或某几种目标函数最优。

（3）每个工件在m台设备加工都有一定的先后顺序，工件在不同设备的加工顺序不同的情况不作考虑以及信息掌握情况和资源约束等适用条件。

（4）举例。建筑施工流水作业问题：在不同的施工段上按一定的施工工艺进行施工，而施工工艺又由不同的施工工序组成，每道施工工序都要消耗一定的人工费用，机械台班和材料费用，并且某些施工工序之间有一定的先后约束关系，如支起模板后才能浇注混凝土，而此问题关注不同施工工序如何搭接排序组成一定施工工艺，使整个施工按照最短施工时间保持一定施工节拍进行流水作业，同时消耗人、机、材等资源也合理。

4、说明C－W节约算法的基本思想，你认为还可用它解决哪些方面的问题？举例加以说明。

解：（1）C－W节约算法的基本思想（以旅行商问题为例）：优先考虑将节约值最大的弧插入到旅行线路中，这样在满足访问若干城市各一次且仅一次的条件下，最大限度地缩短了路程。

（2）举例。运用C－W节约算法：设n个不同用户为n个点，维修点为基点，n个用户点中从点i到点j的长度为工人骑摩托车的交通时间加上点i与点j维修时间总和的一半。优先考虑将节约值最大的长度加入工作线路中去进行迭代。

内容来源	胡运权《运筹学教程》（第5版）配套题库

5、说明本书所述货运车辆优化调度算法的原理和求解步骤，并绘出求解过程框图。请简要回答以下问题：

（1）若有两种车型的车可用，书中提出的模型应怎样修改？在书中所提算法的启发下，试拟定一套求解的迭代步骤。

（2）如何将书中提出的模型和算法推广到多目标的情形？

解：（1）货运车辆优化调度算法的原理：最小费用最大流原理。求解步骤为：①仅考虑重载点，运用表上作业法求出最优解作为原问题的可行解；②进行解的扩展和解的收缩，直至得到可接受的可行解；③以该可接受的可行解为依据确定初始行车线路；④根据具体约束条件进行调整，直至得到最优行车路线。求解过程框图如图2-14-1所示。

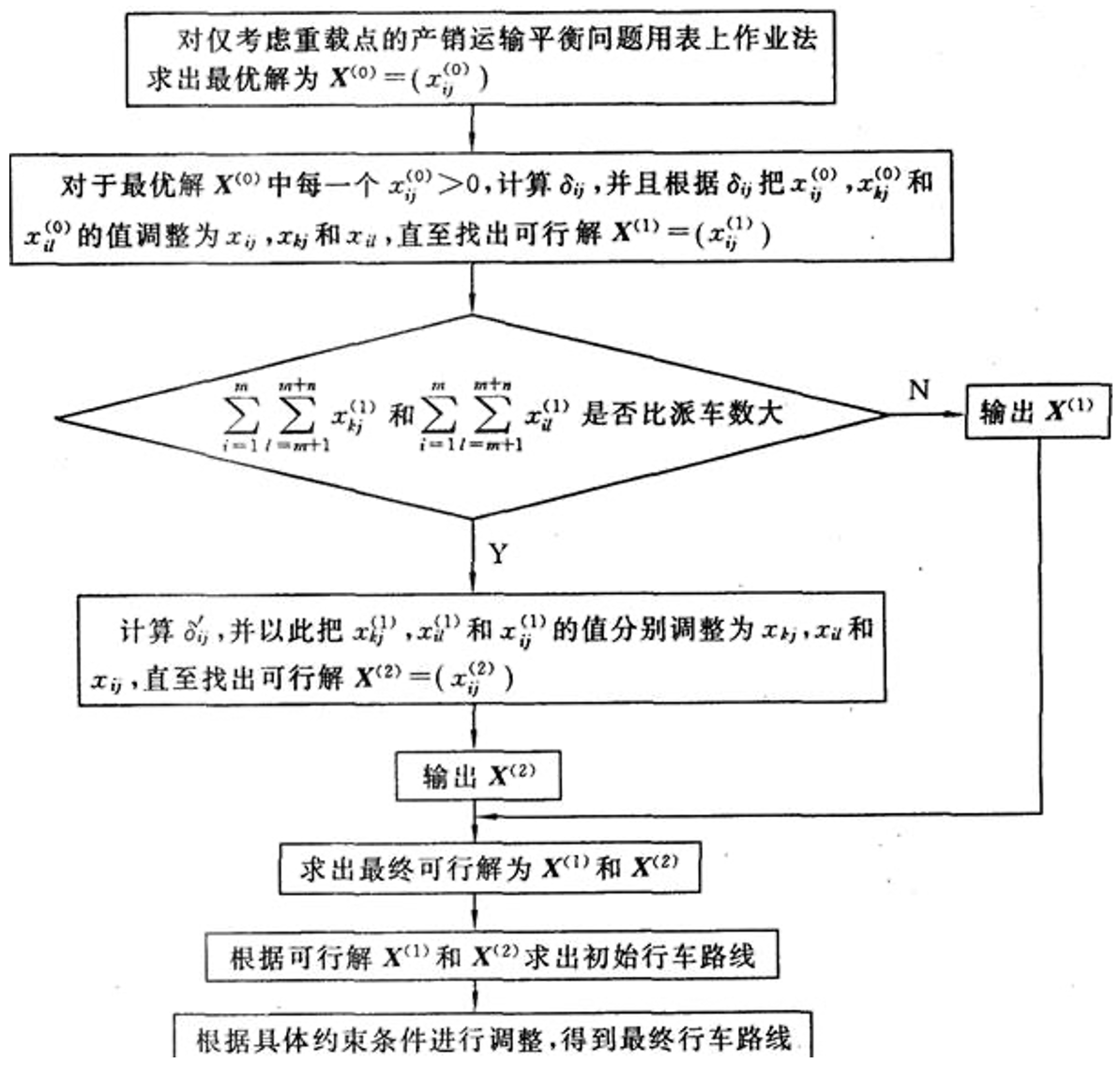
图2-14-1

（2）修改后的迭代算法即神经网络（neural networks）算法。

①建立结合矩阵：将车辆经过的点包括源点看成神经网络的结点，即神经元，令神经元数目为N；i神经元和j神经元的结合权值为ω_ij，j神经元的输出为r_j。

②将车辆调度的各种约束条件转化为约束能量函数为E_约。

③神经网络计算：令时刻t神经元i的输出为r_i（t），且r_i（t）只能取0或1，令神经元i的阈值为Q_i，则输出能量为E_输＝f（r_i（t），Q_i，ω_ij），因此总的能量函数为E_总＝E_输＋E_约。如果r（t＋∆t）＝r（t），其中∆t＞0，则该网络相对处于稳定状态。由于∆E＜0，且E有界，系统必趋向一个比较好的稳定状态，再把此稳定状态时r_i（t）形成换位阵中元素为1的结点连接起来，形成所求的最满意车辆调度线路。

④根据所形成的最满意线路来选择车辆调度方案。

（3）推广到多目标情形：车辆优化的目标函数可以有很多个，如总运费最小，司机总的驾驶时间最短，车辆满载行驶的时间最长等；而约束条件，如路径的最大输入输出流、车载量、发车和收车约束等。也可以加入惩罚算子将约束条件转化为惩罚函数，利用多目标方法进行求解。

6、表2-14-1给出了12个工件在设备A和B上的加工时间，要求：

（1）若所有工件都先在设备A上加工，再在设备B上加工，试安排使总加工时间最短的工件加工顺序，并计算总加工时间。

（2）若工件8～12先在设备B上加工，再在设备A上加工，其他条件同上，请设计一启发式算法，以确定尽可能小的总加工时间和安排相应的工件加工顺序。

表2-14-1

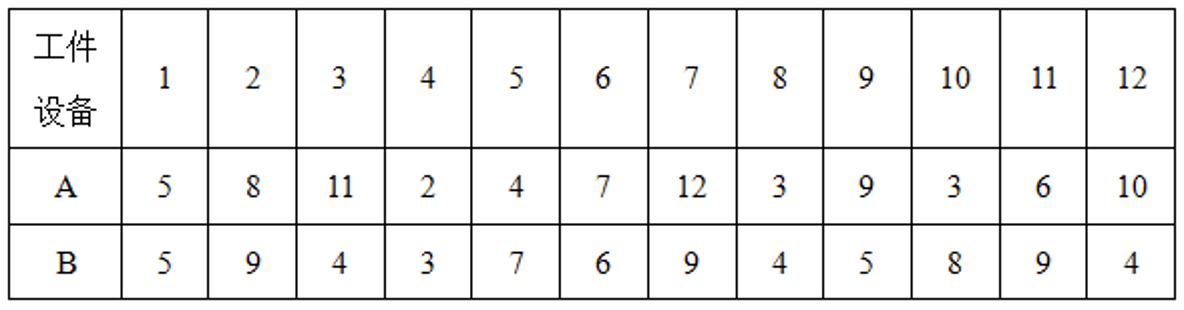
解：（1）采用启发式算法进行计算，计算过程如表2-14-2所示。

表2-14-2

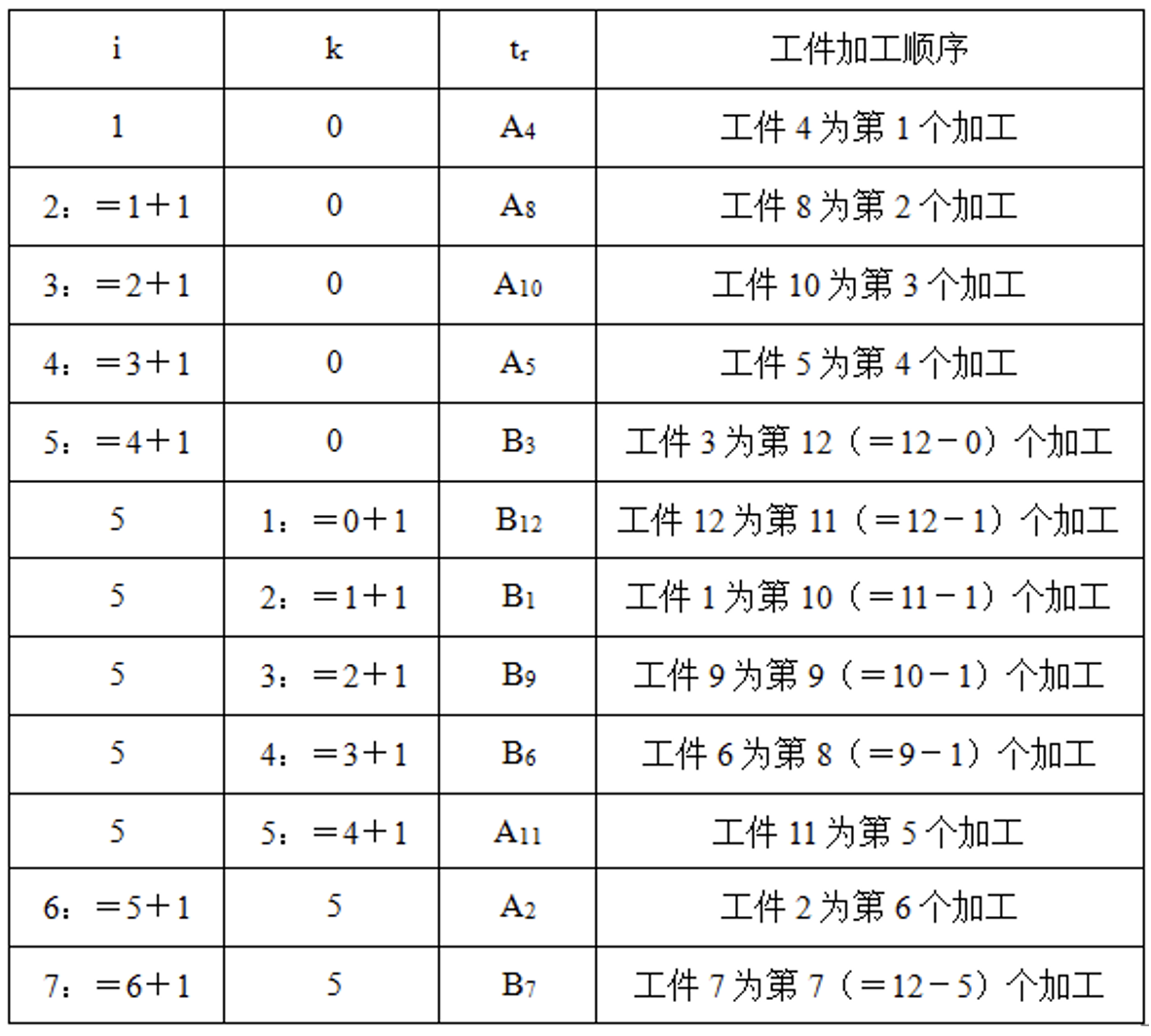
由上表可以看出，总加工时间最短的工件加工顺序为

4→8→10→5→11→2→7→6→9→1→12→3

总加工时间为（2＋3＋3＋4＋6＋8＋12＋7＋9＋5＋10＋11）＋4＝84。

（2）可设计如下启发式算法：

①i_A＝i_B＝1，k_A＝k_B＝0；

②t_r1＝max{A₁，A₂，…，A₇，B₈，B₉，…，B₁₂}，t_r2＝min{B₁，B₂，…，B₇，A₈，A₉，…，A₁₂}；

③若t_r1＝A_j（j＝1，2，…，7），则工件j为A设备的第i_A个加工工件，并置i_A：＝i_A＋1；

若t_r1＝B_j（j＝8，9，…，12），则工件j为B设备的第i_B个加工工件，并置i_B：＝i_B＋1；

若t_r2＝A_j（j＝8，9，…，12），则工件j为A设备的第12－k_A个加工工件，并置k_A：＝k_A＋1；

若t_r2＝B_j（j＝1，2，…，7），则工件j为B设备的第12－k_B个加工工件，并置k_B：＝k_B＋1；

④将A_j，B_j删去，即不再考虑已排好加工顺序的工件j；

⑤转入步骤②，直至步骤②中的工件加工时间表变成空集。

故设备A最优加工顺序为7→2→5→6→1→3→4→12→9→11→10→8，

设备B最优加工顺序为12→9→11→10→8→7→2→5→6→1→3→4；

总加工时间为（12＋8＋4＋7＋5＋11＋2）＋（10＋9＋6＋3＋3）＝49＋31＝80。

……

【完整版】 达聪网 胡运权《运筹学教程》（第5版）配套题库【考研真题精选＋课后习题＋章节题库】

  热门内容

2023年运筹学考研题库（含考研真题）

运筹学教材编写组《运筹学》（第4版）配套题库【名校考研真题＋课后习题＋章节题库＋模拟试题】

全国自考《运筹学基础（课程代码：02375）》历年真题汇编（含部分答案）